n=3
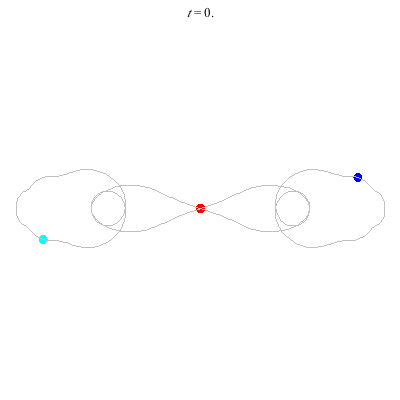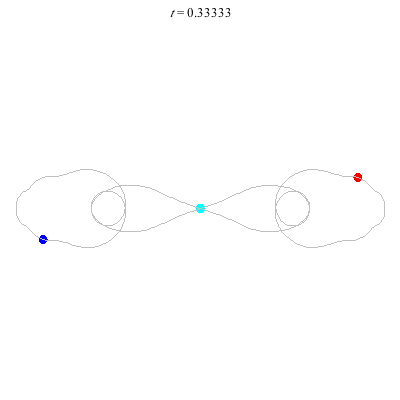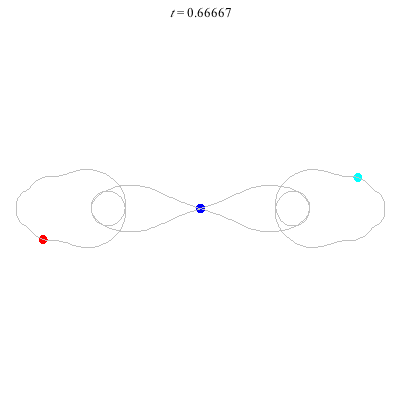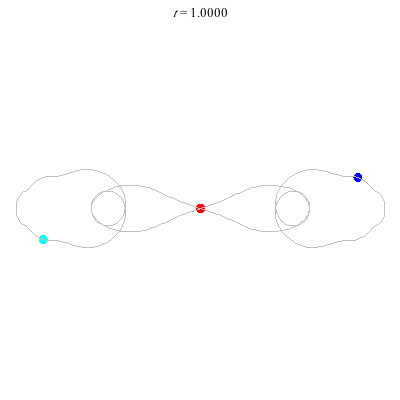
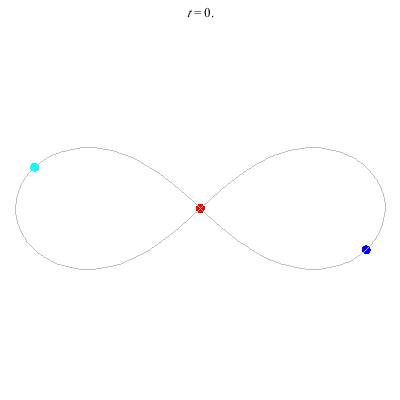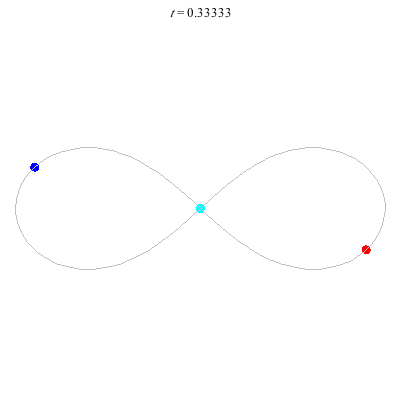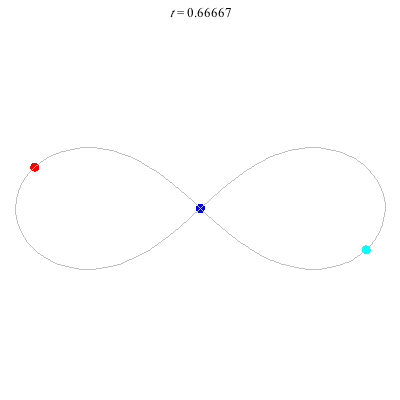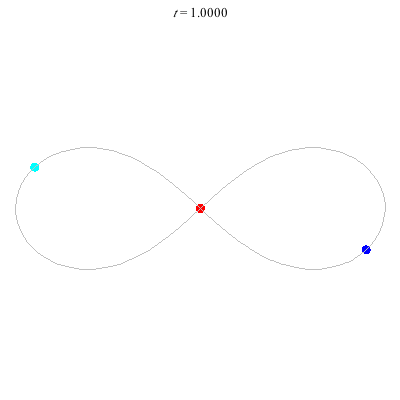
D'(3,2)
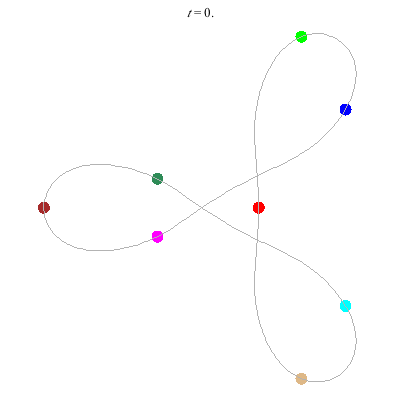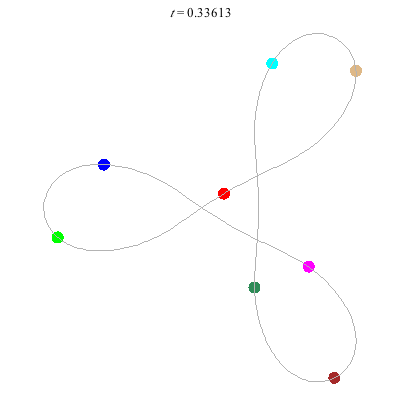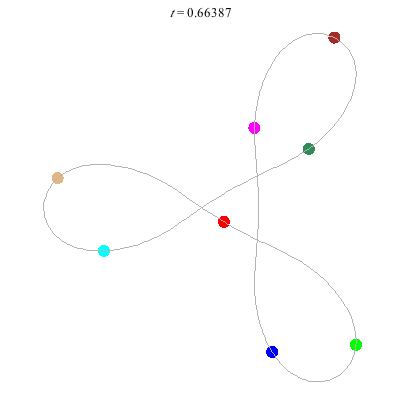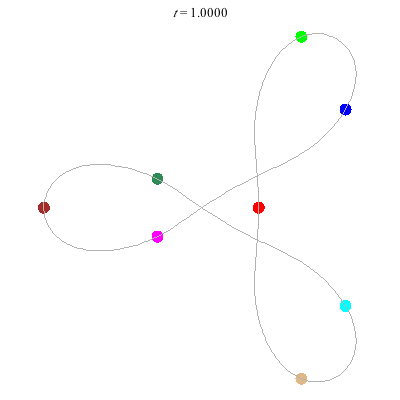
- Figure 8
- winding nos = (-, 0).
- with extra twist
- winding nos = (-, 0).
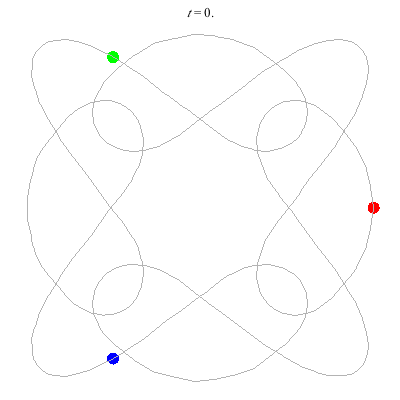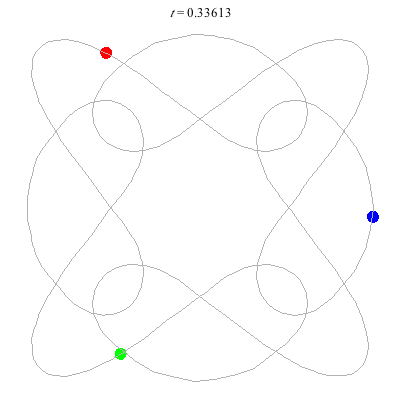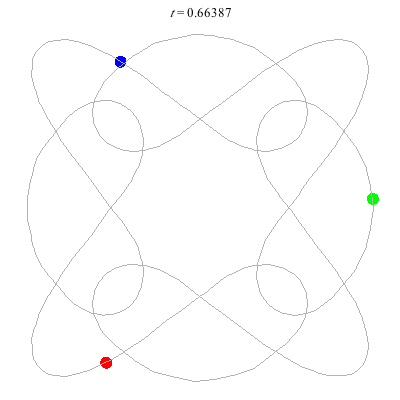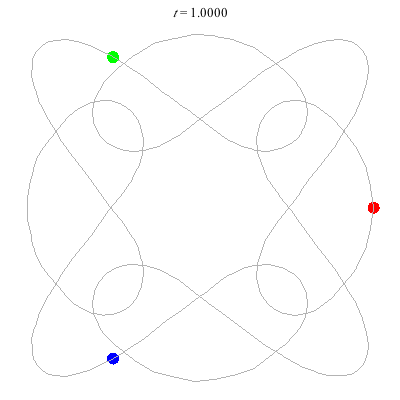
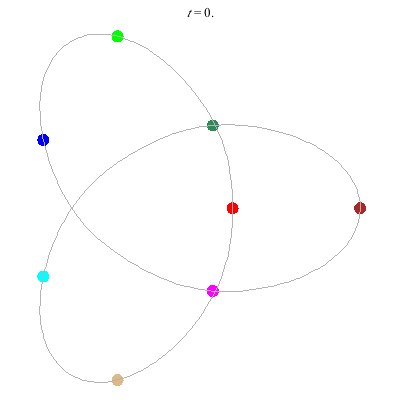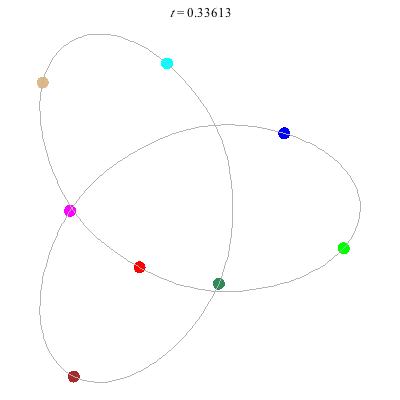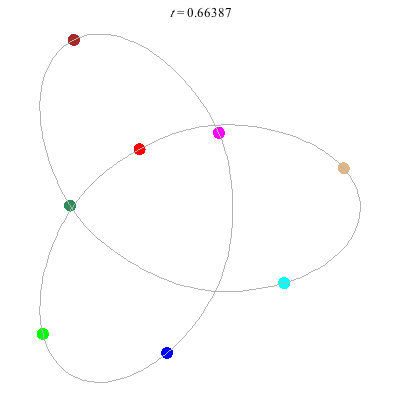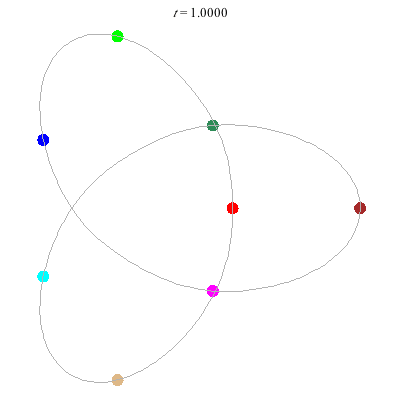
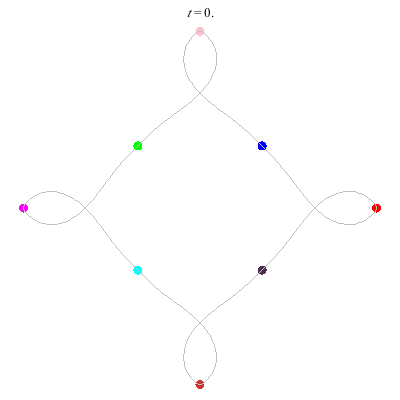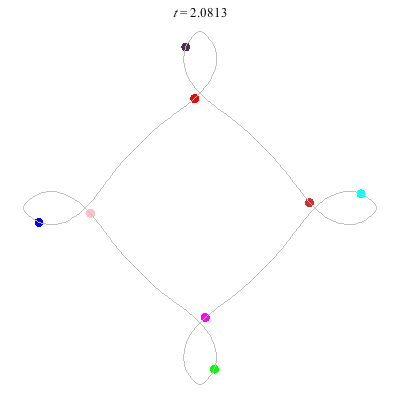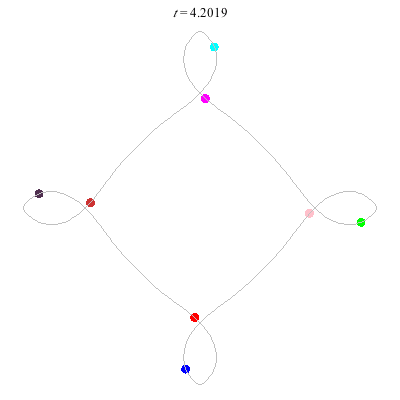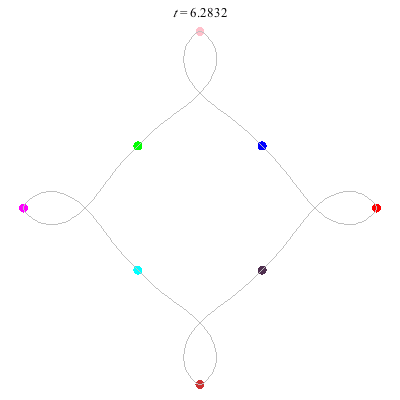
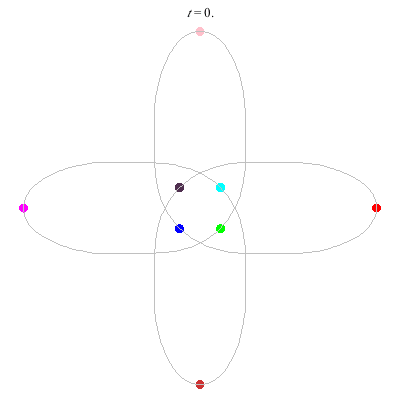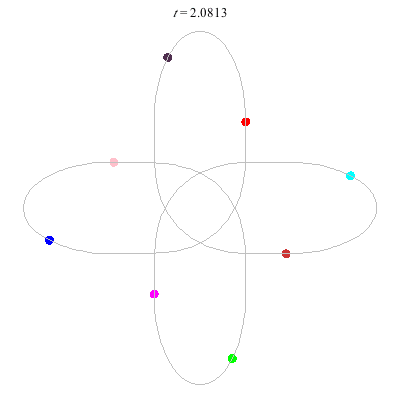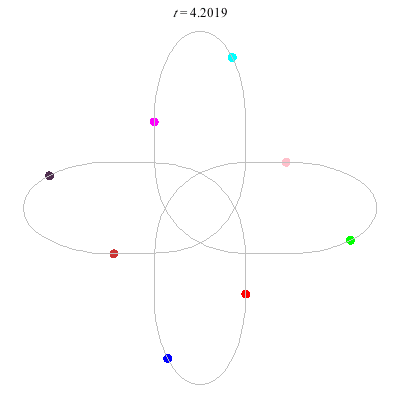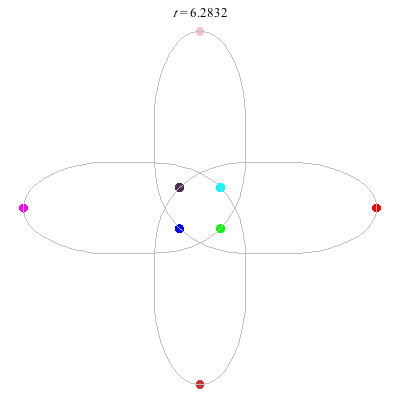
D(3,4)
- New and gorgeous! A Celtic knot !
- Still a bit wobbly even with FS=30 - should try matlab?
- winding nos = (1; -3).
D(3,5) - wishful thinking!
n=4
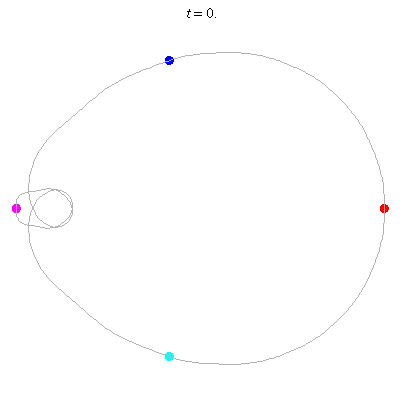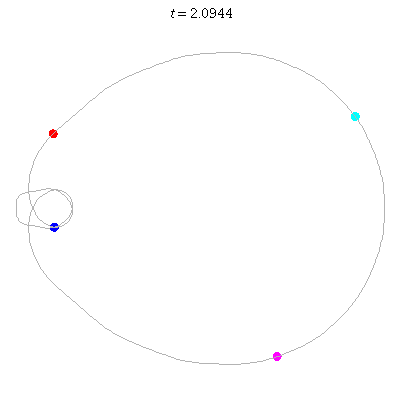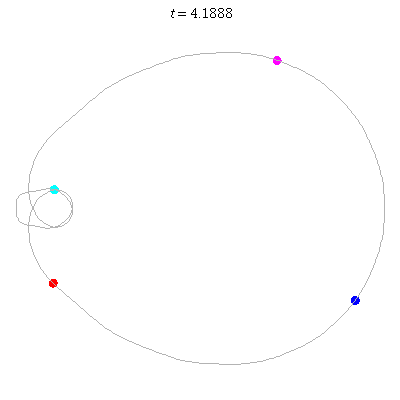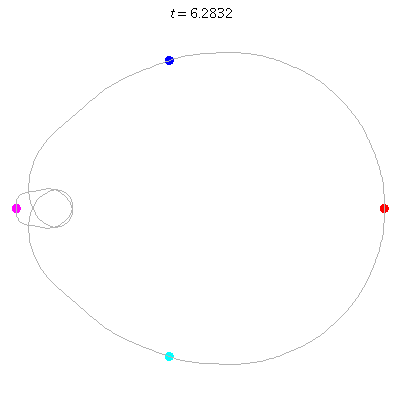
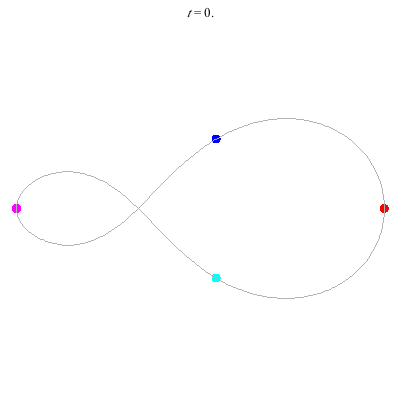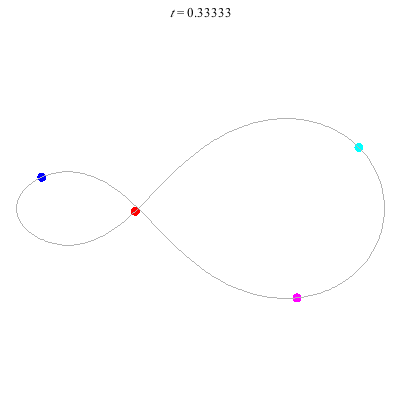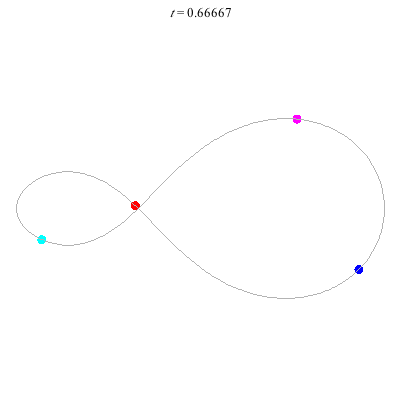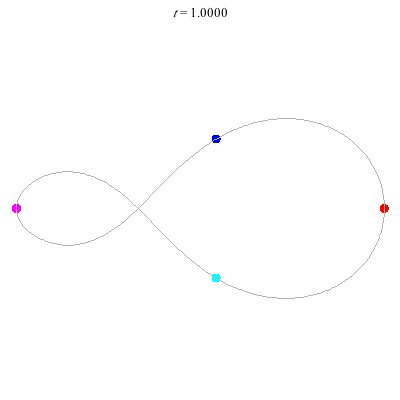
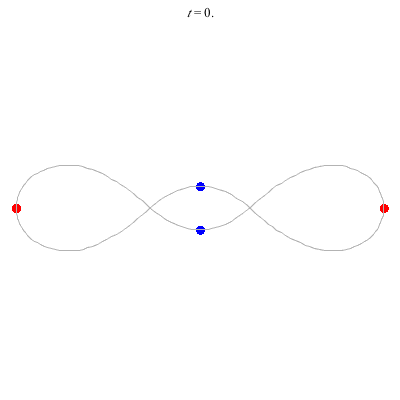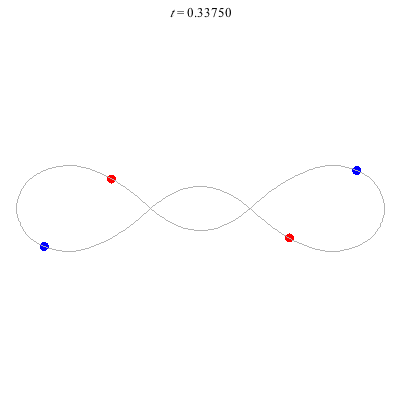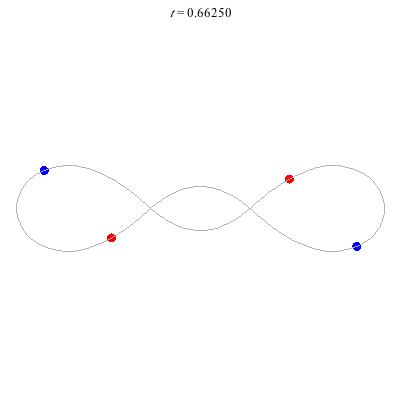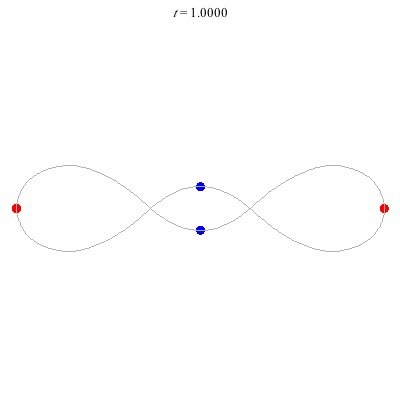
D(4,1)
- Off-centre figure 8.
- ''winding nos =" -1; 0, -1
- With extra twist
- ''winding nos =" 1; 2, 1
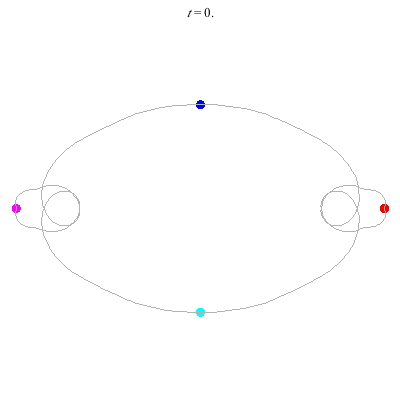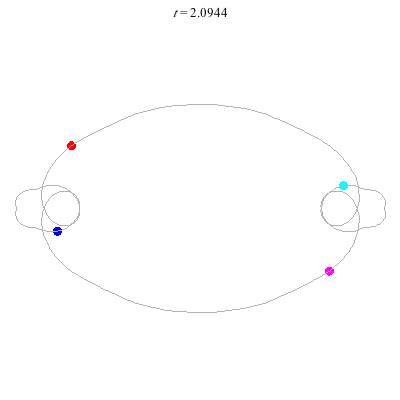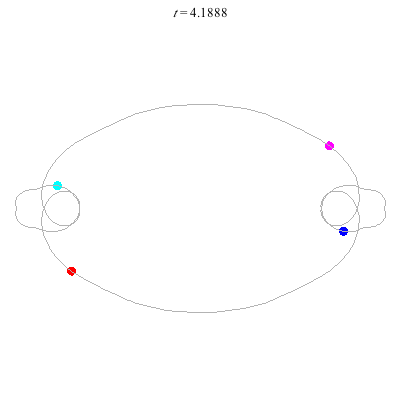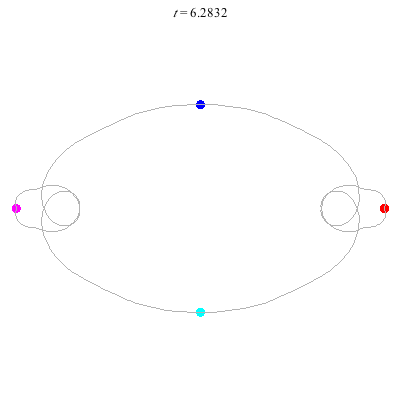
D(4,2)
- Gerver's solution
- winding nos = -1; 1, -1
- With extra twist
- winding nos =
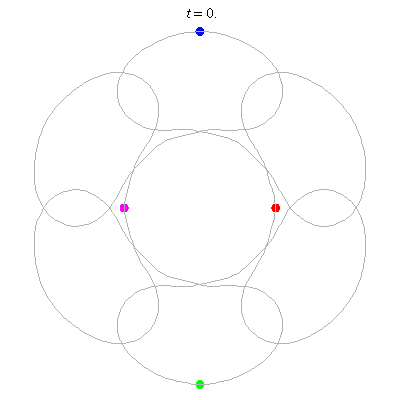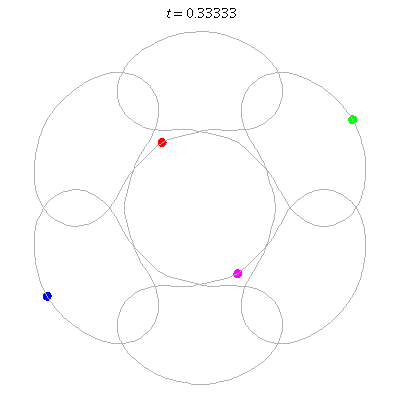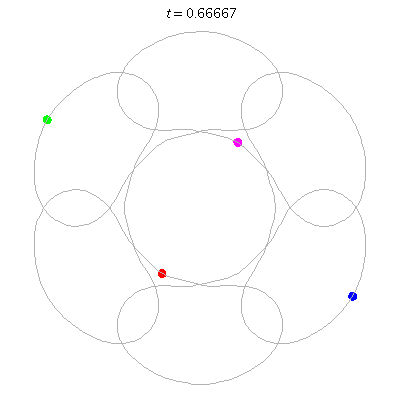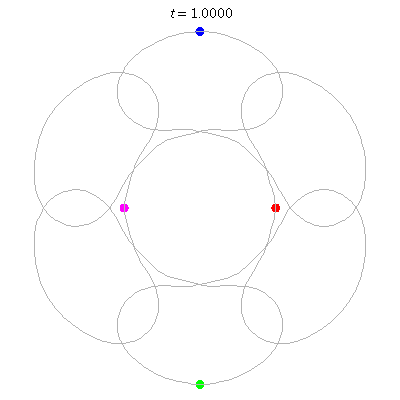
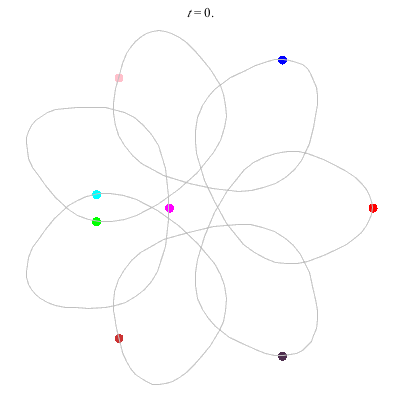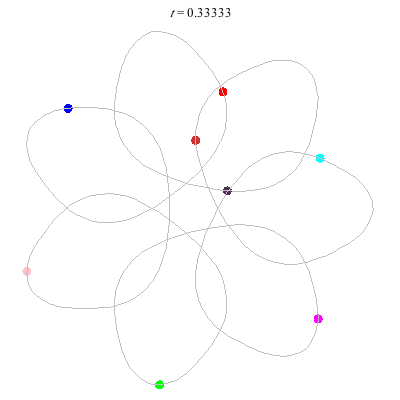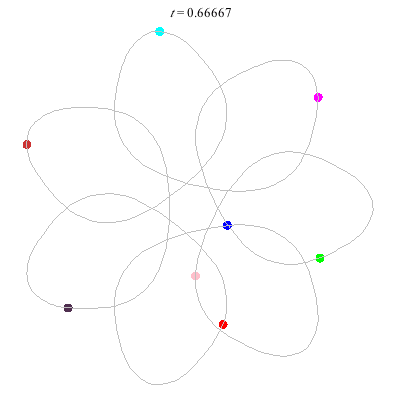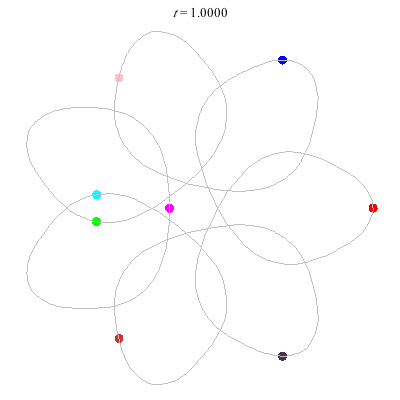
D(4,6)
- Beautiful: 6 ovals around a central hexagon.
n=5
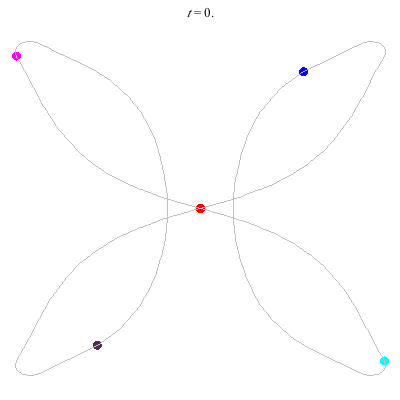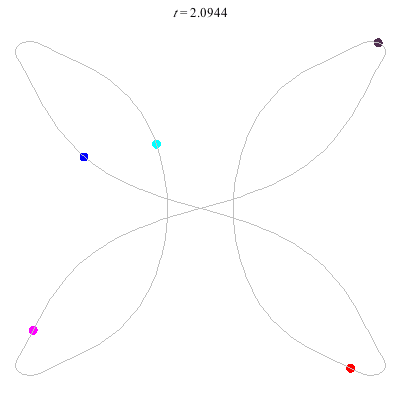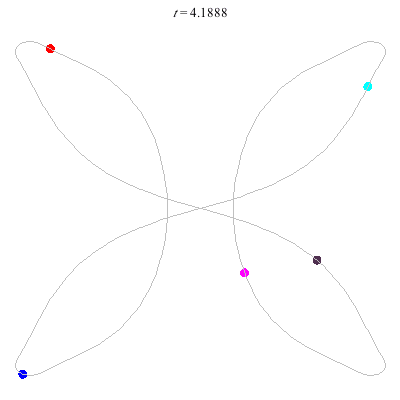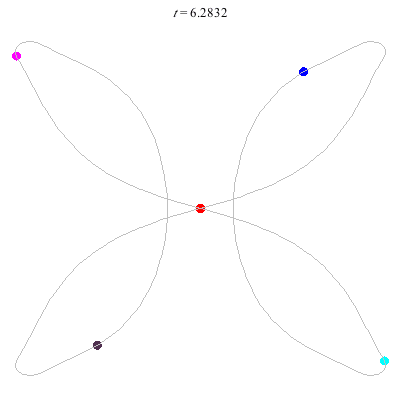
D'(5,2)
- Bowtie example.
- - also many examples in paper of Simo
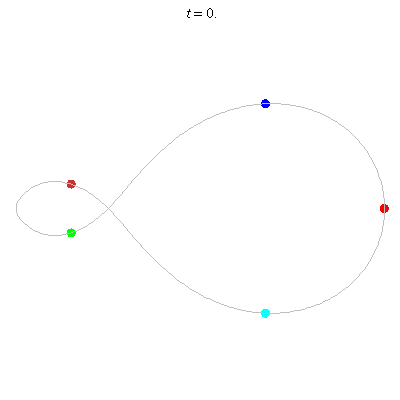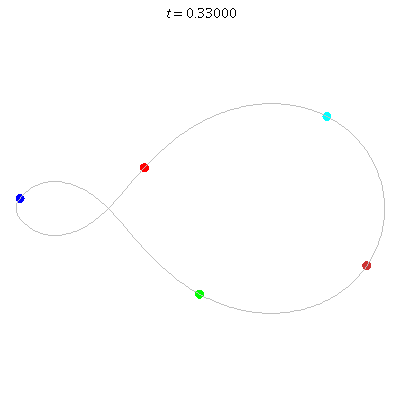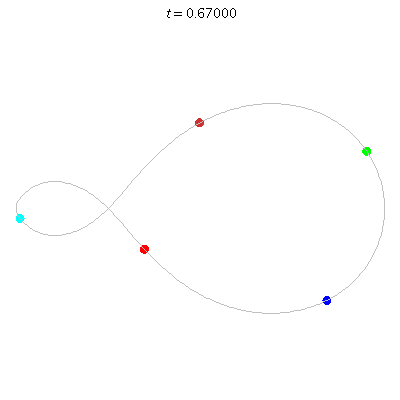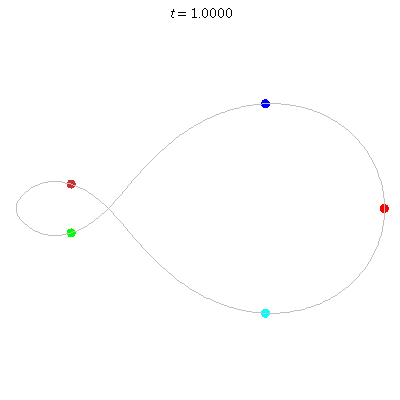
D(5,1)
- Skew Fig. 8.
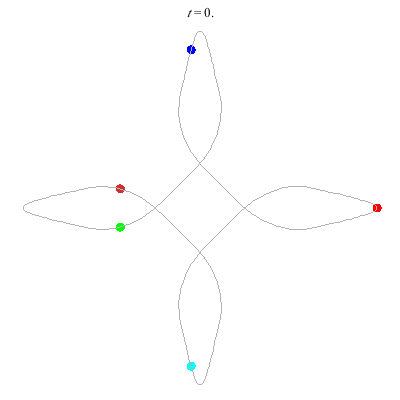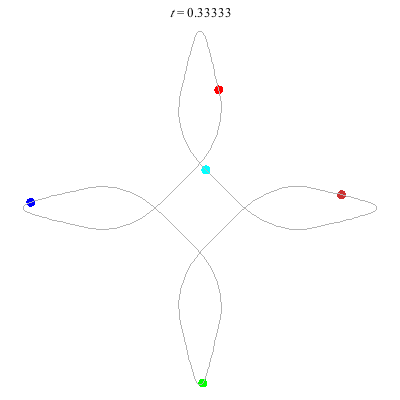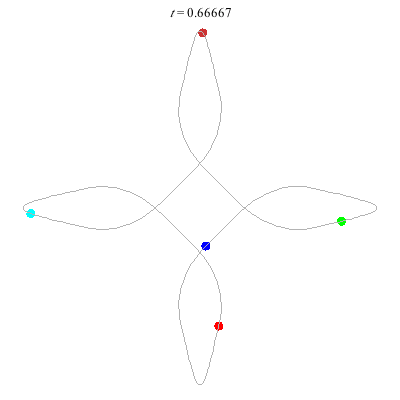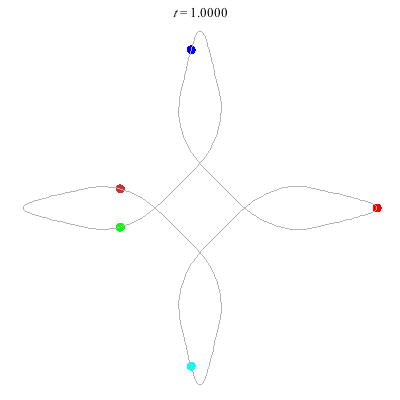
D(5,4)
- 5 on a 4-daisy.
- winding nos: 1, -3, ??
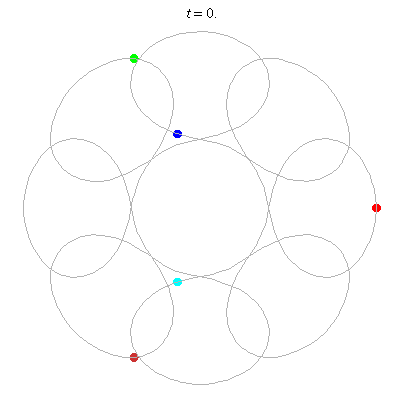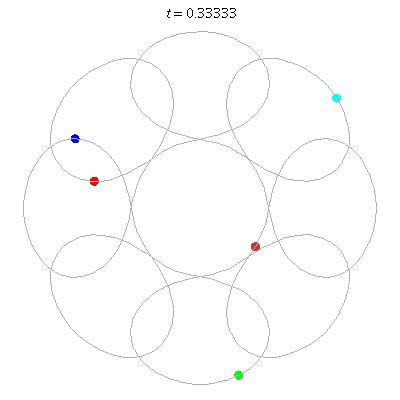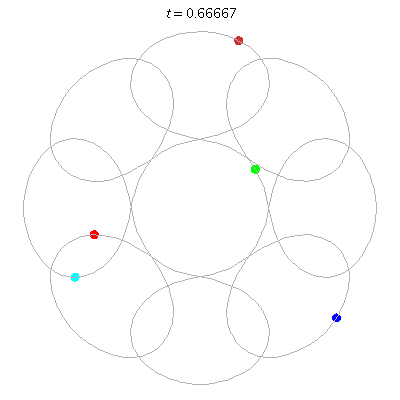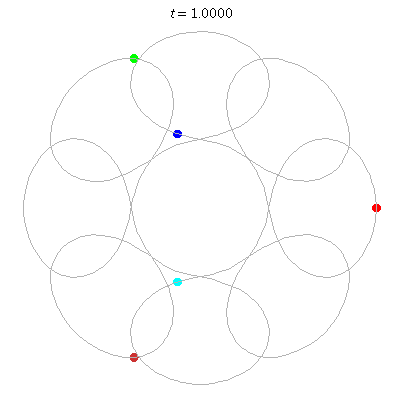
D(5,8)
- circular chain with 8 links
- winding nos: 1; -7, 1
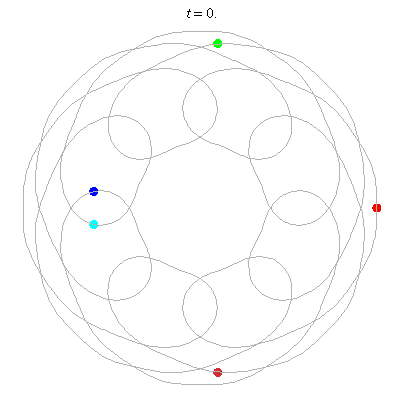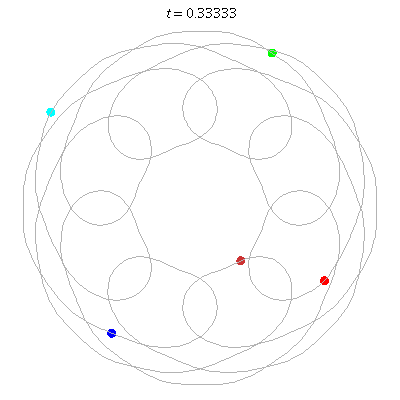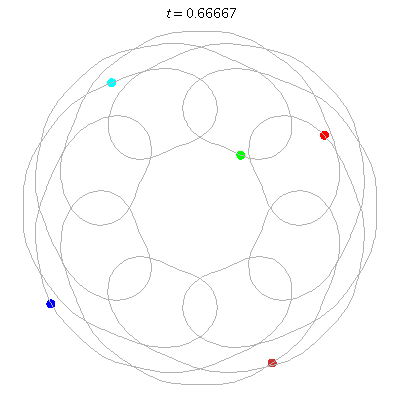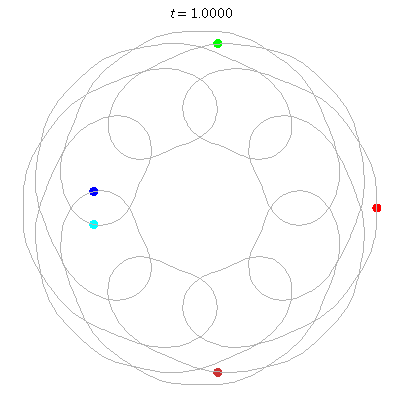
D(5,8/3)
- 5 on an 8-flower
n=6
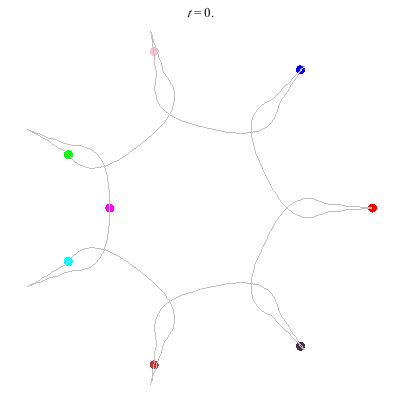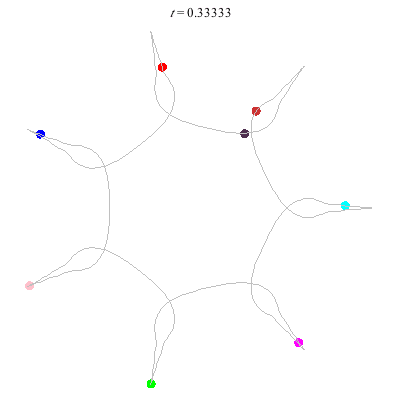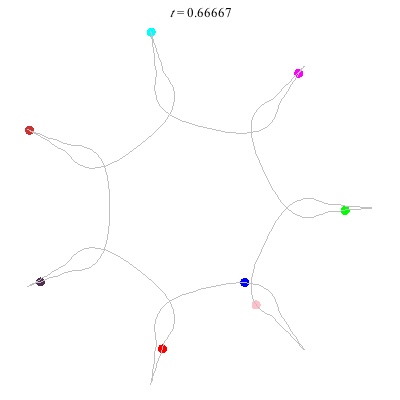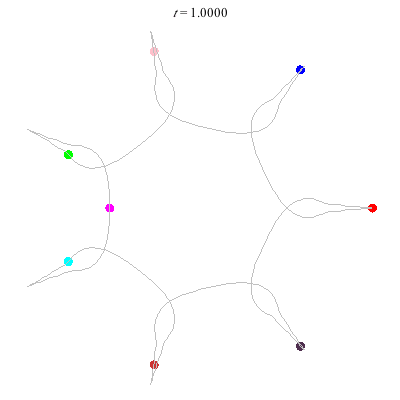
The D(6,∞,1) (circular choreography) has
- winding nos = (1; 1, 1, 1), and
- action = 84.5.
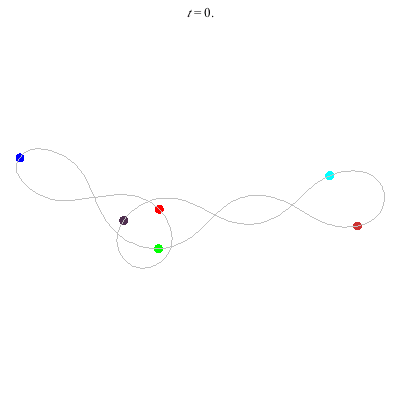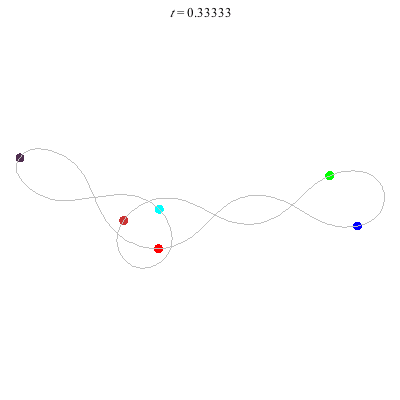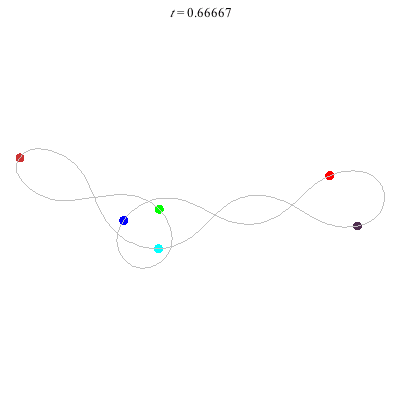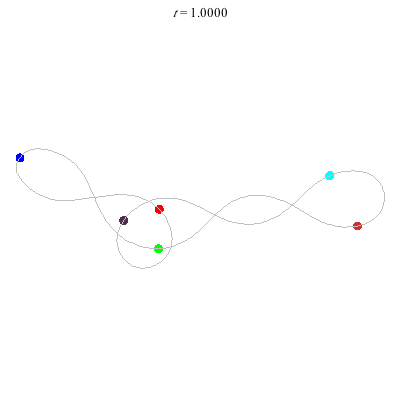
C(6,1)
- no symmetry (Simo)
- winding nos = (1; 1, 0, 1)
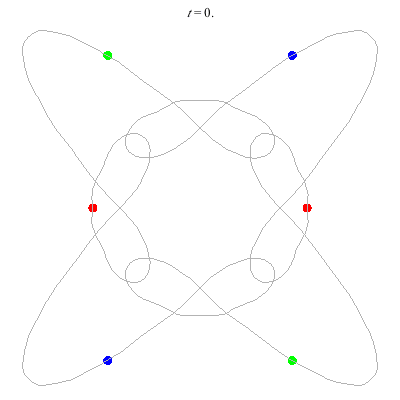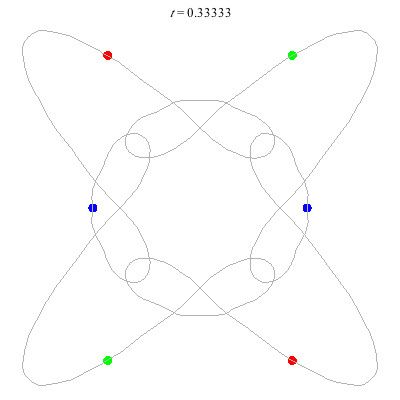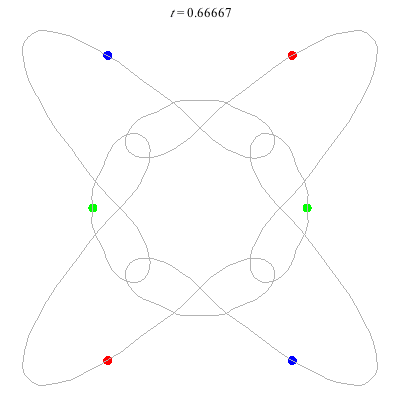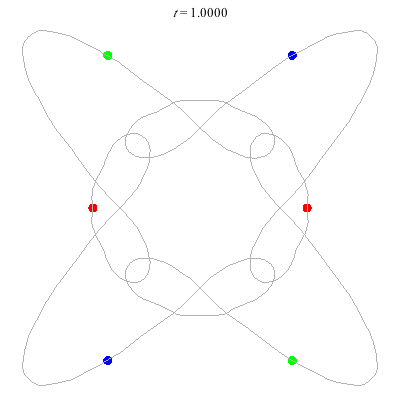
(c)
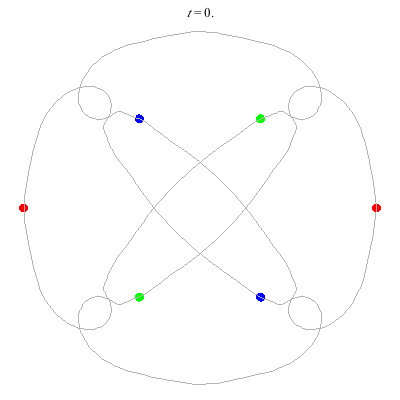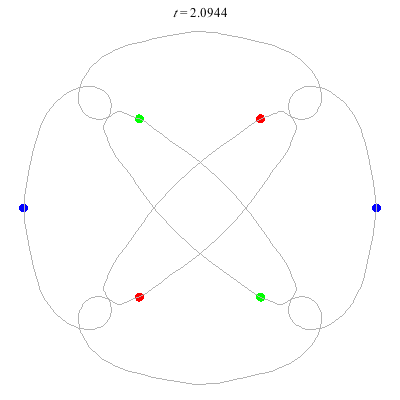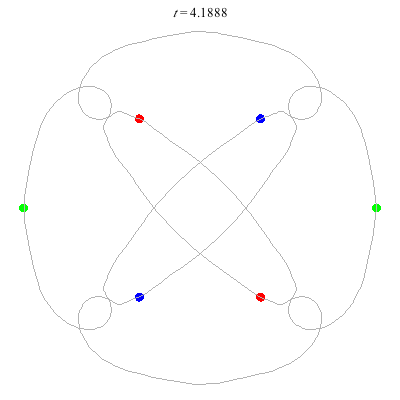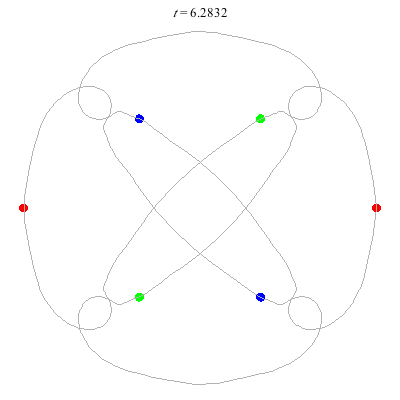
(b)
(a)
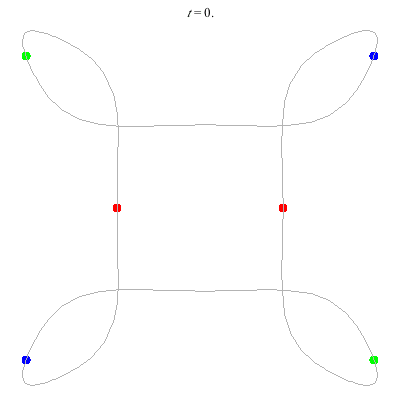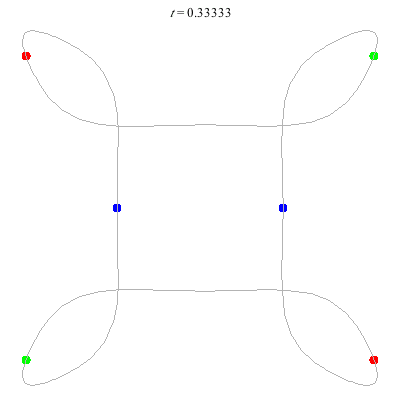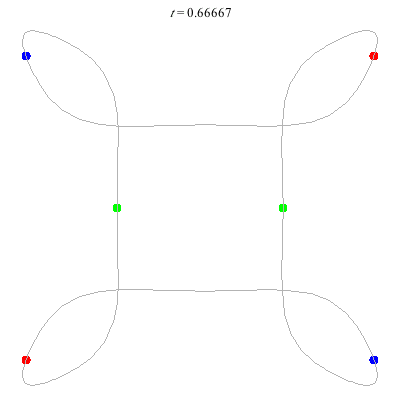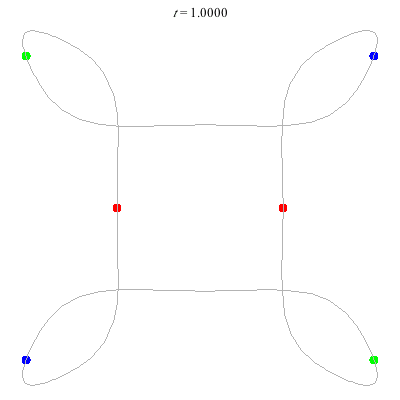
D(6,4) This has core of order 2.
- (a) A square with loops at vertices.
- Action=136
- winding nos = (1; -3, 1, 1).
- (b) A square with diagonals.
- Action=227
- winding nos = (1; -3, -3, 1).
- (c) Doubling up D(3,4) ...
- Action=220
- winding nos = (1; 1, -3, 1).
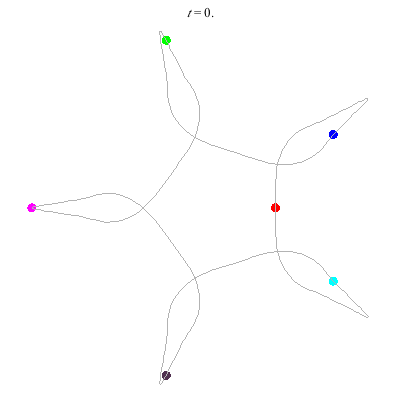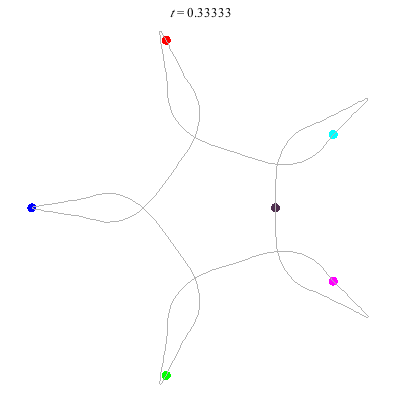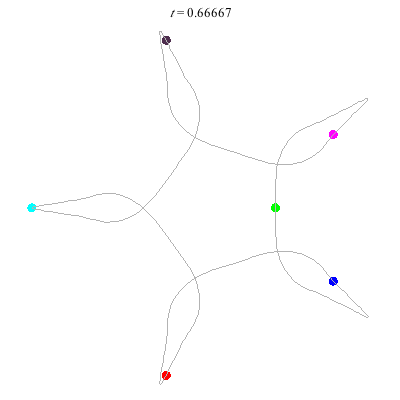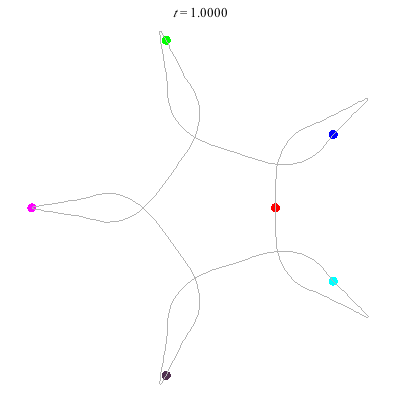
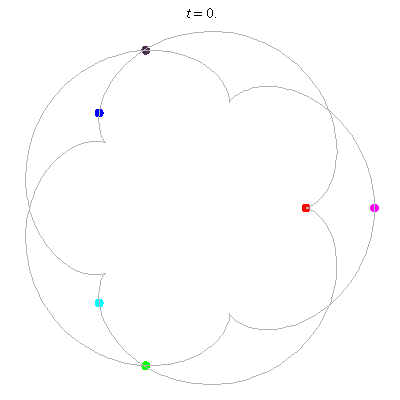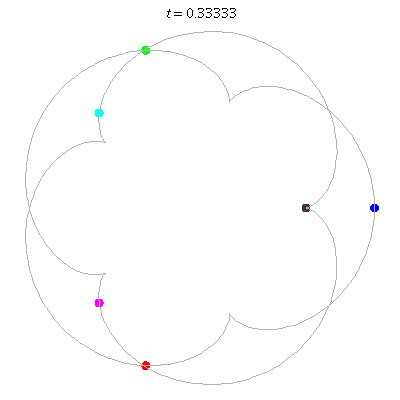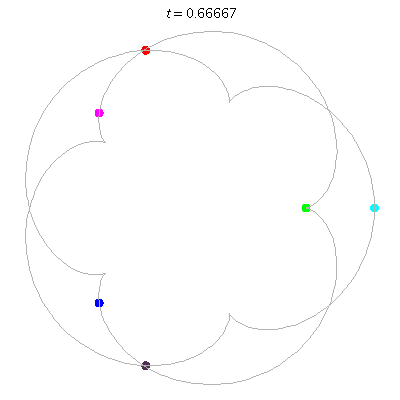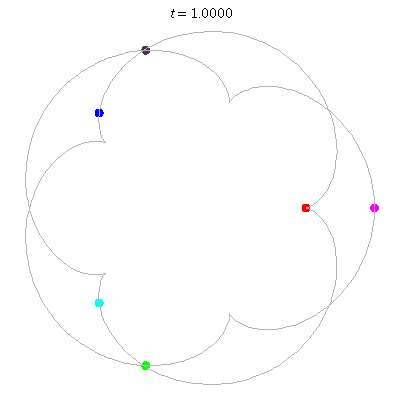
D(6,5)
- 6 on a daisy (pentagon with loops).
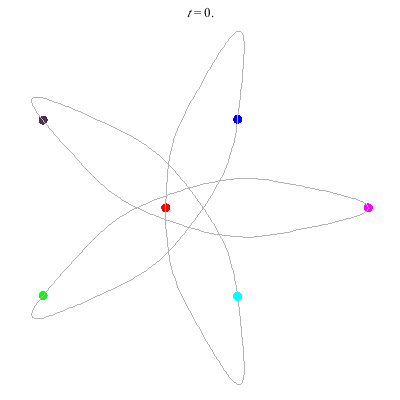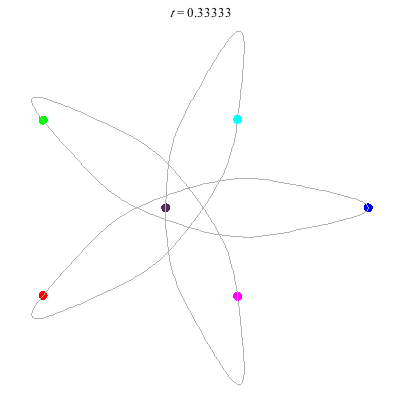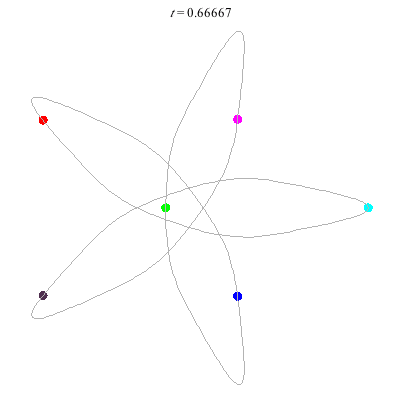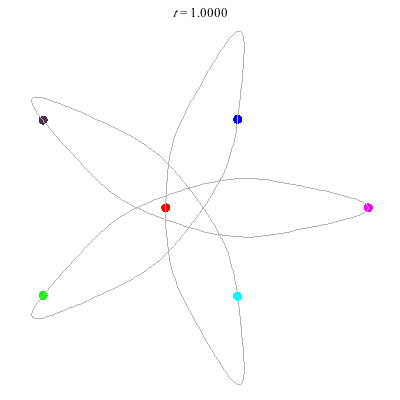
D(6,5/2)
- (a) a pentagram?
- winding no. (-3; -3, 2, -3).
- (b) round a circle
- winding no. (2; 2, 2, 7).
heptagons and heptagrams:
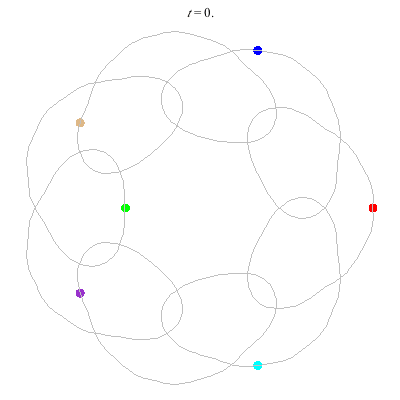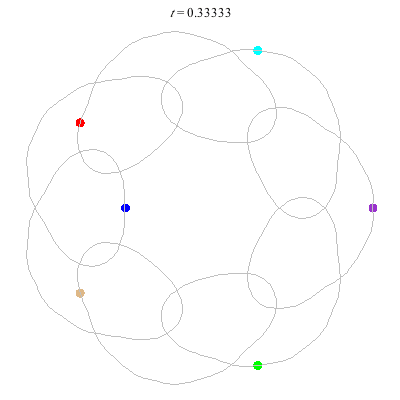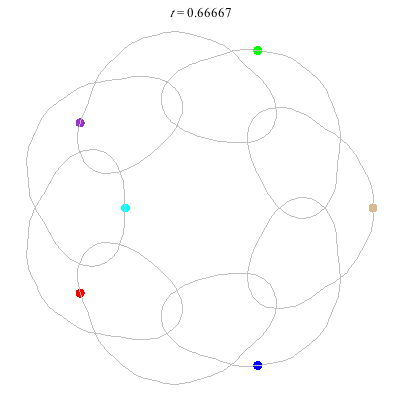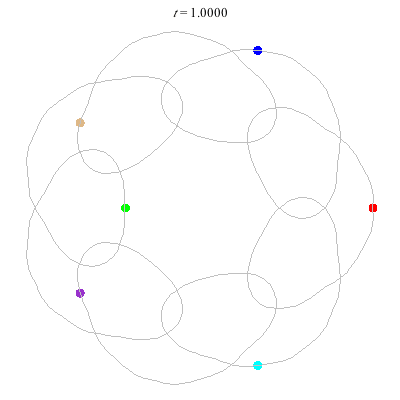
D(6,7)
- Heptagon chain with 'inward links'
- winding nos = (1; 8, 1, 1)
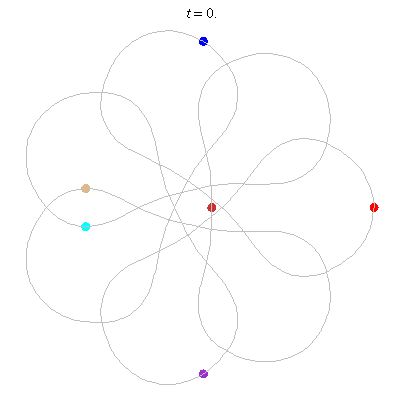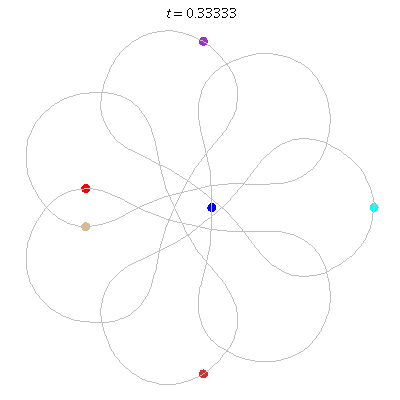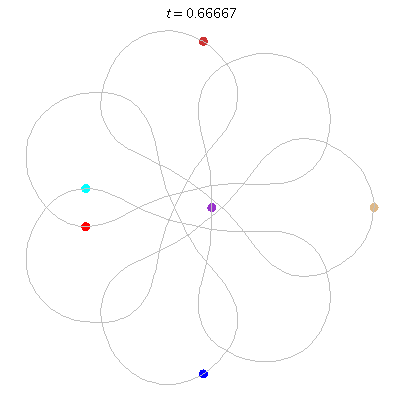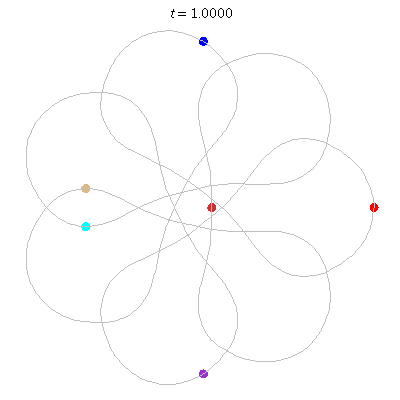
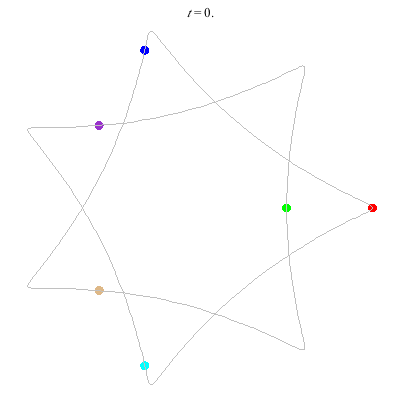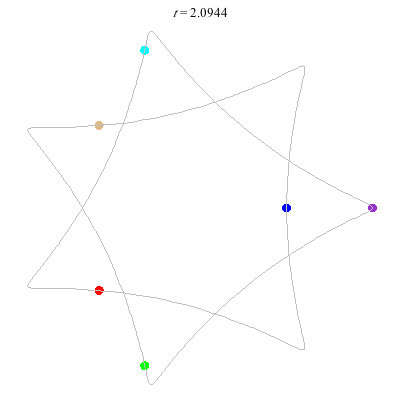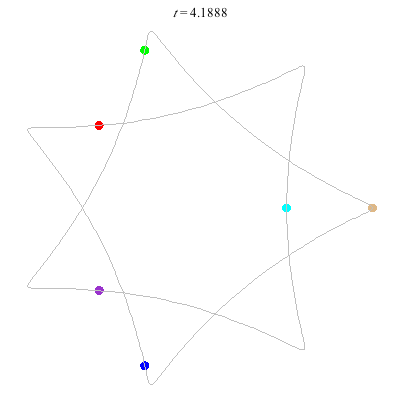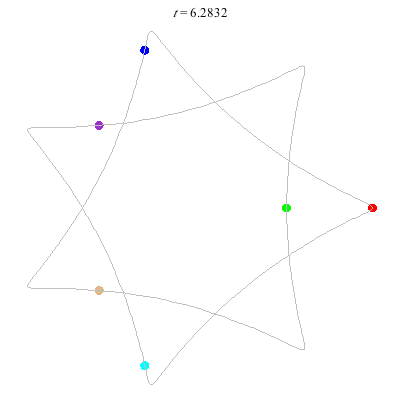
D(6,7/2)
- (a) Simple heptagram
- winding nos = (2; 2, 2, -5)
- (b) on 7 petals
- winding nos = (2; 2, -5, -5)
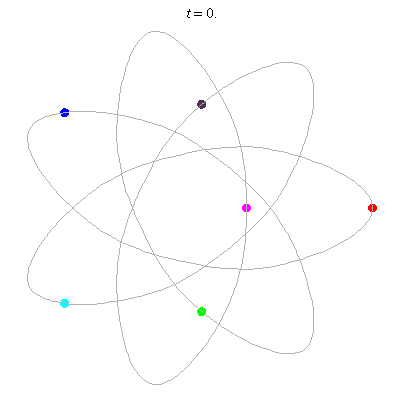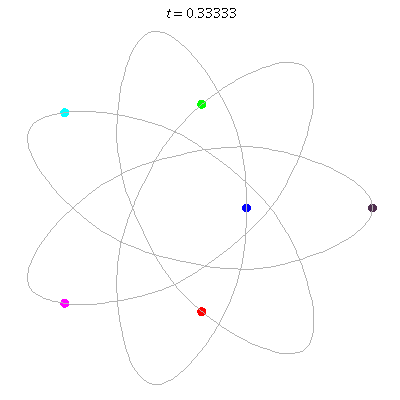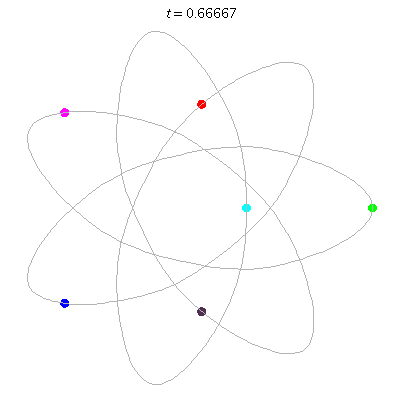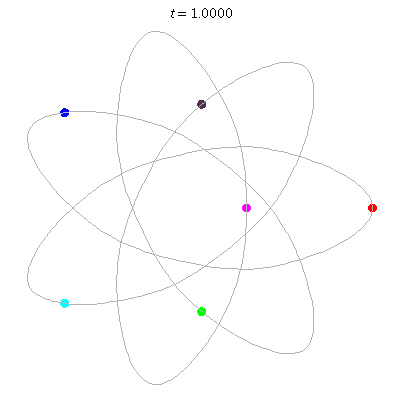
D(6,7/3)
- on a {7/3} heptagram,
- winding nos = (-4; -4, -4, 3).
n=7
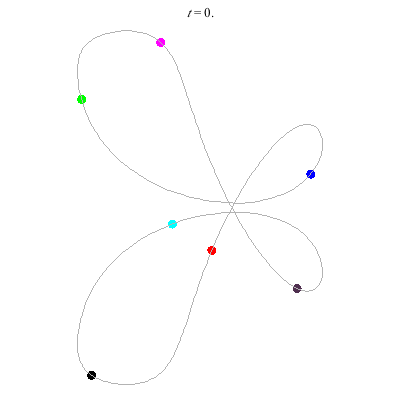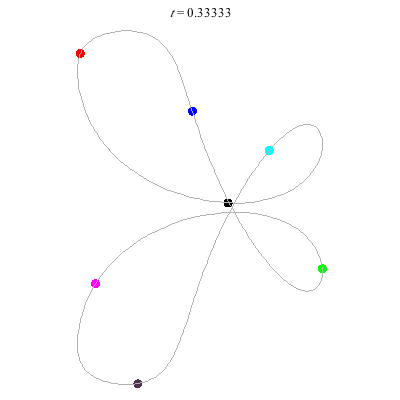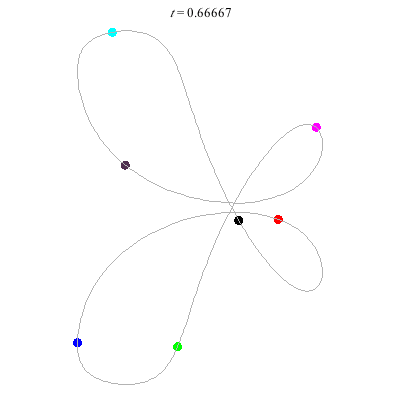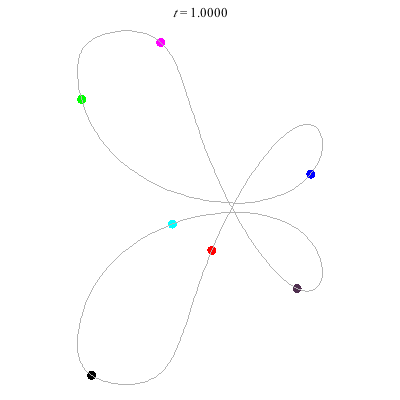
C'(7,2)
- Reflection but not time-reversing:
- Thm: winding nos = 0.
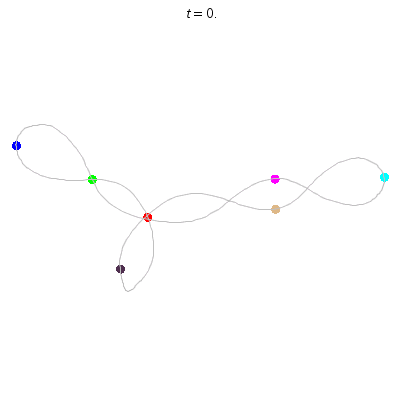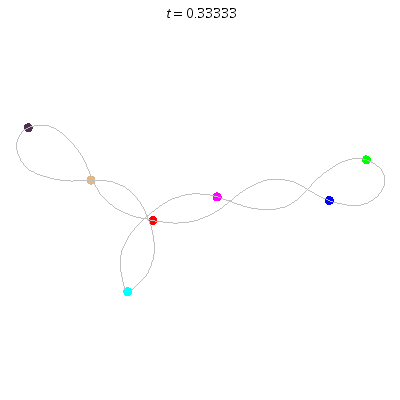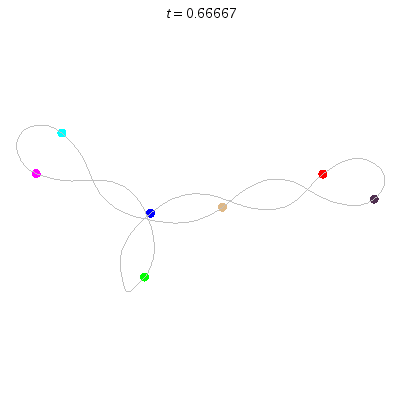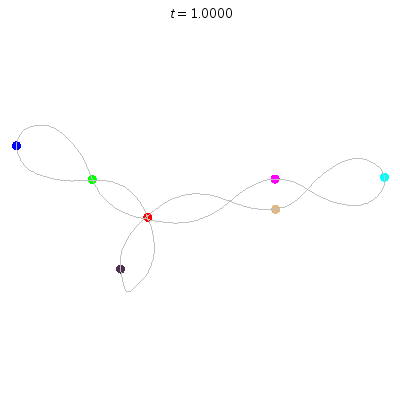
C(7,1)
- no symmetry
- winding nos = 1; 1, 0, 0.
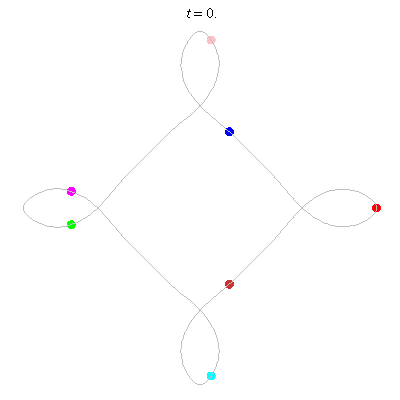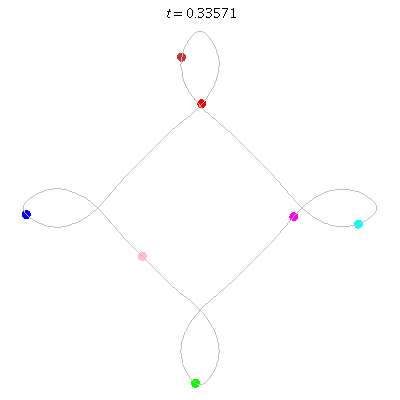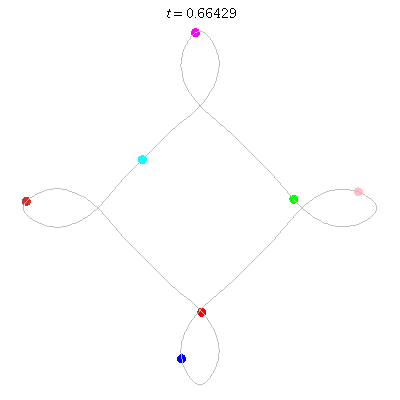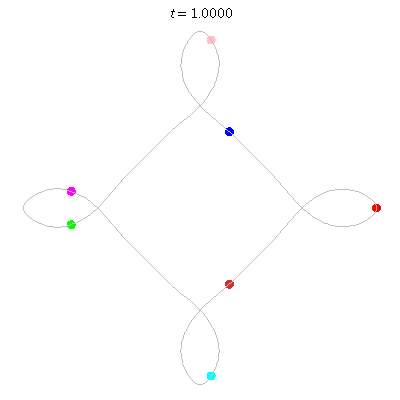
D(7,4)
- seven on ...
- winding nos = .
n=8
(b)
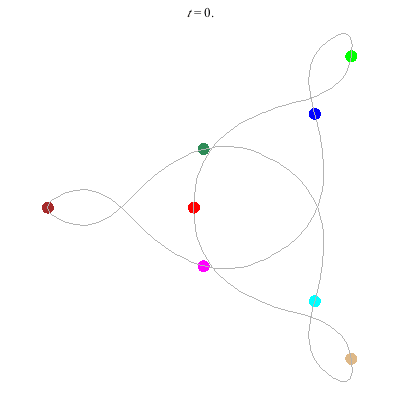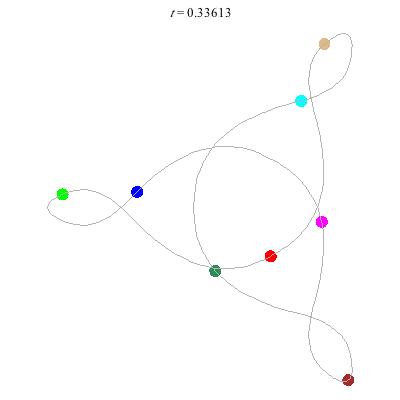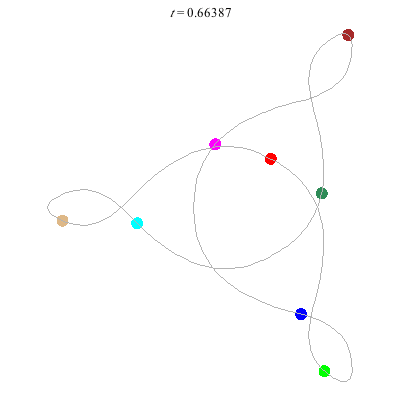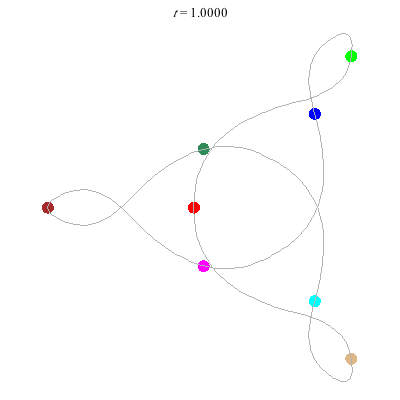
(a)
D(8,3)
- (a) Moustache
- Action= 264
- winding nos = -2; 1, -2, -2, 1.
- (b)
- Action= 217
- winding nos = 1 ; -2, -2, 1, 1.
(d)
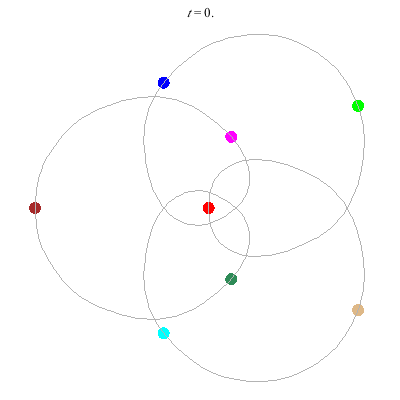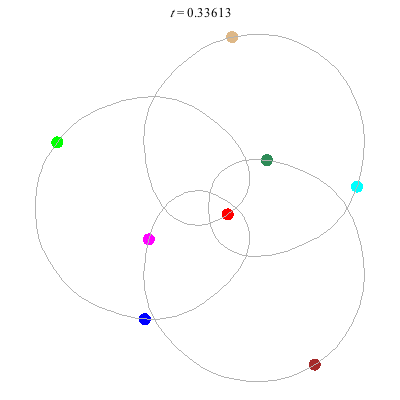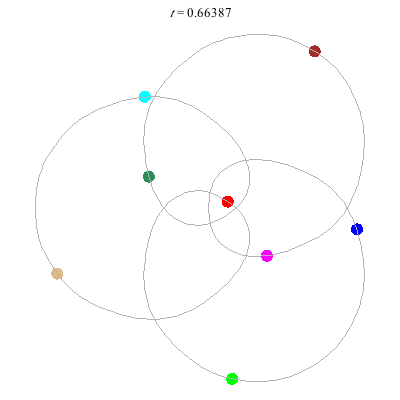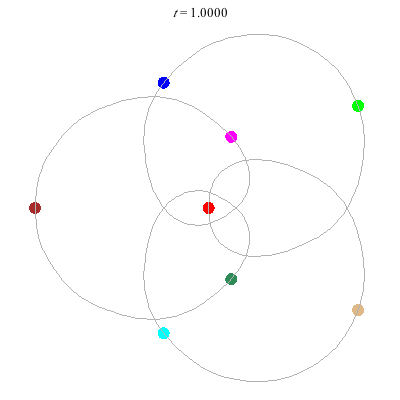
(c)
- (c)
- Action= 304
- winding nos = 4 ; 4, 1, 4, 1.
- (d)
- Action= 227
- winding nos = -2; -2, -2, -2, 1.
For comparison, action for D(8,∞) is 150.
(b)
(a)
D(8,4) - order 4 core
- (a) 4 balloons
- Action = 281
- winding nos = -3; -3, -3, 1, -3.
- (b) Square with loops
- Action =
- winding nos = 1; ?.
(b)
(a)
D(8,7)
- (a) 8 on 7-petalled flower
- Action = 396 ?
- winding nos = 1; -6, -6, 1, 1.
- (b) 8 on 7-daisy
- Action = 325
- winding nos = 1; -6, 1, 1, 1.
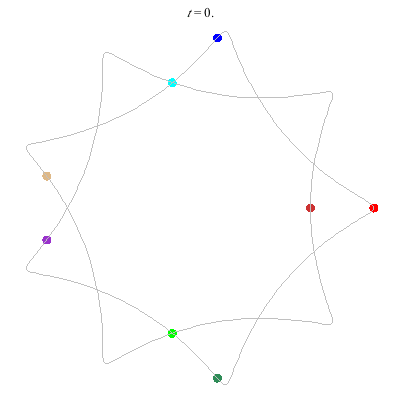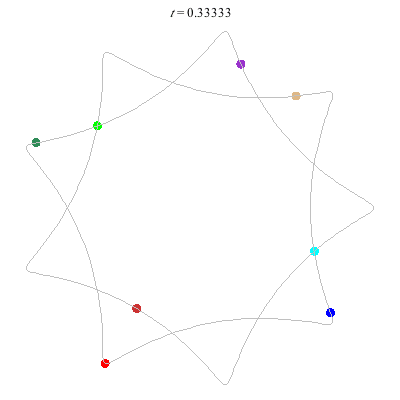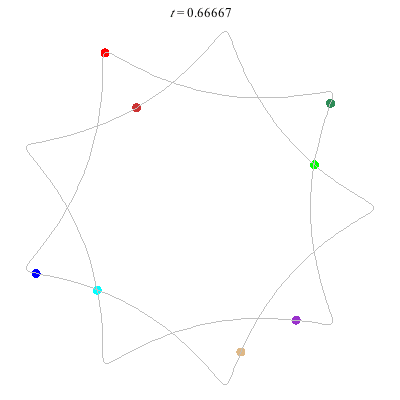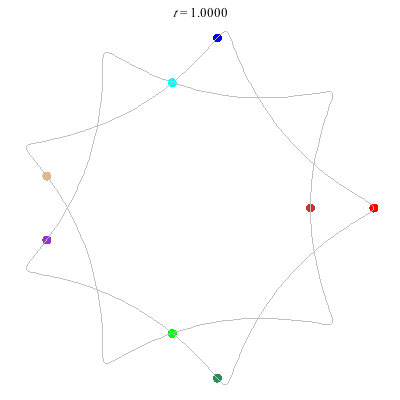
D(8,9/2)
- {9/2}-enneagram
- winding nos = .
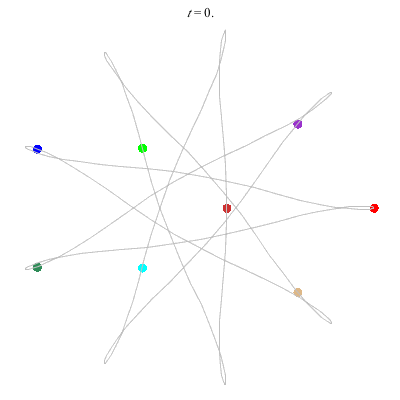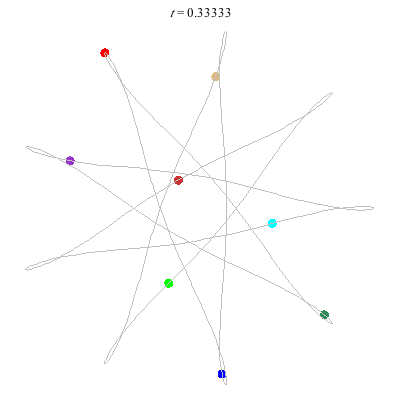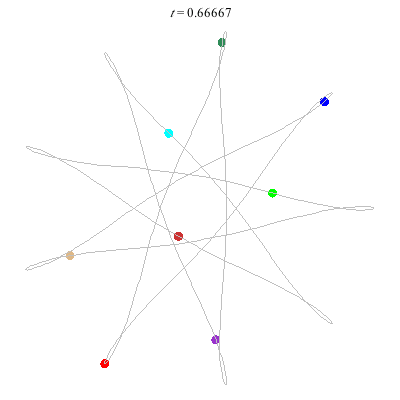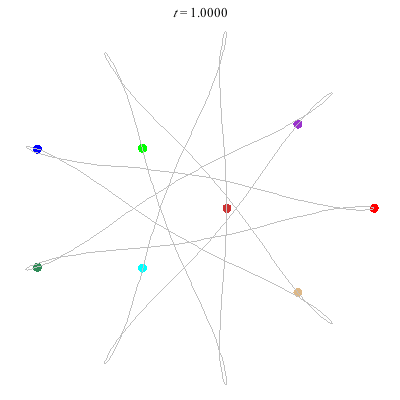
D(8,9/4)
- {9/4}-enneagram
- winding nos = .
n=9
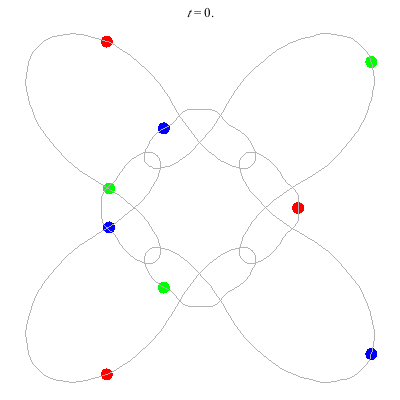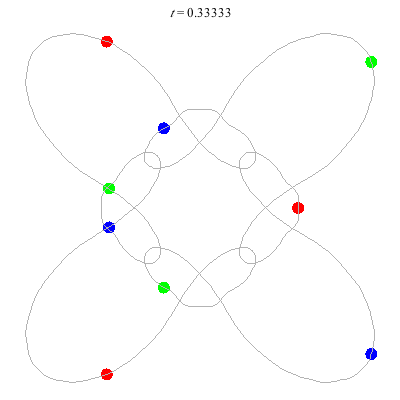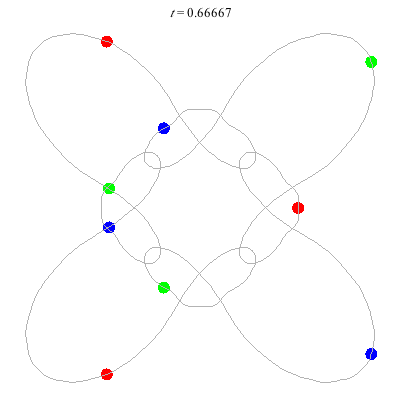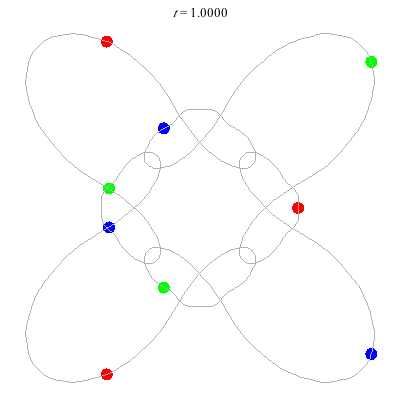
(b)
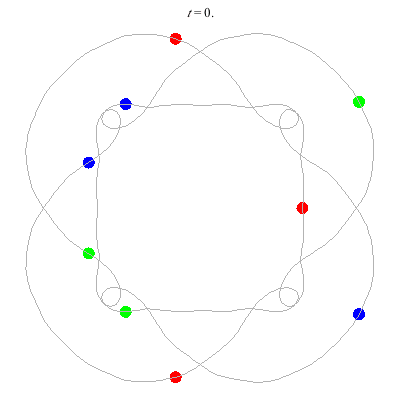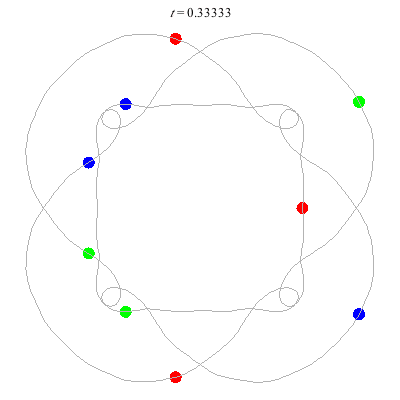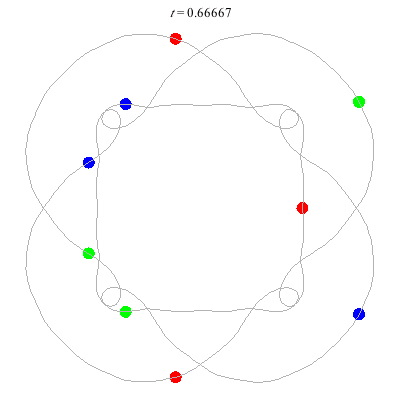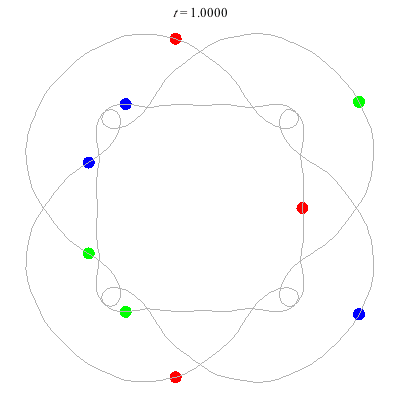
(a)
D(9,4)
- (a) From D(3,4) -
- action = 426
- winding nos = 1; 5, 1, -3, 1.
- (b) From D(6,4) -
- action = 483
- winding nos = 1; 1, 1, -3, 1.
Compare: action for D(9,∞/1) is 189
n=10
Attach:D-10-5.gif Δ|(a) D(10,5)
- (a) 5 balloons
- action =
- winding nos = -4; -4, -4, 1, -4, 1.
Compare: action for D(9,∞/1) is 189
- D(10,5) (b) seems unlikely, with the motion almost a circle, and with increased number of terms I can't get it to converge! See figure
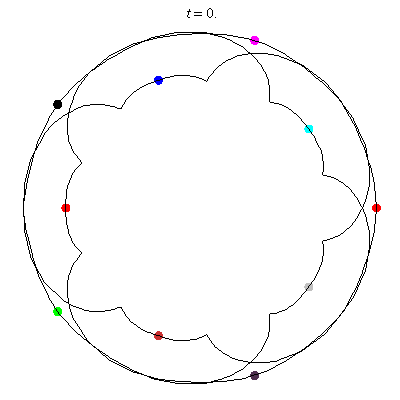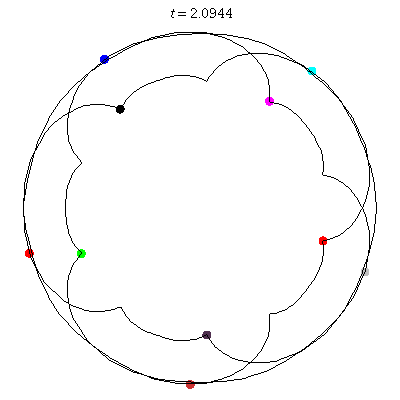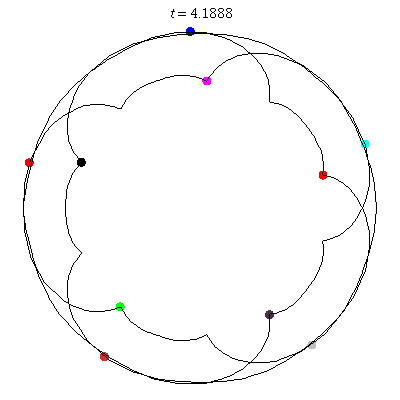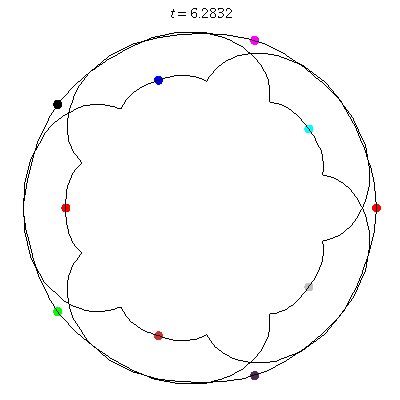
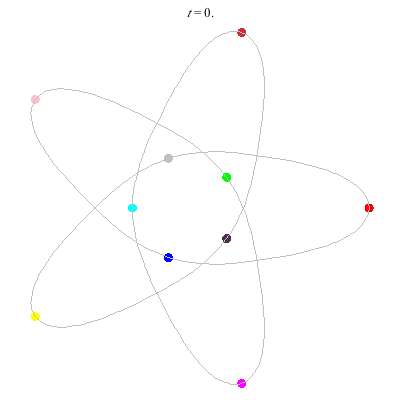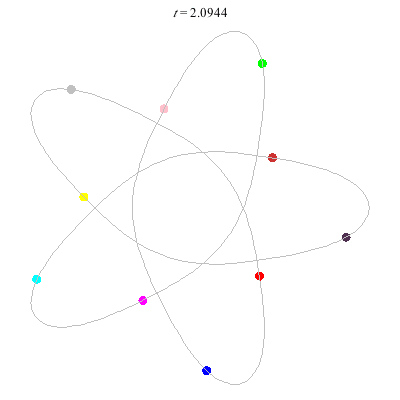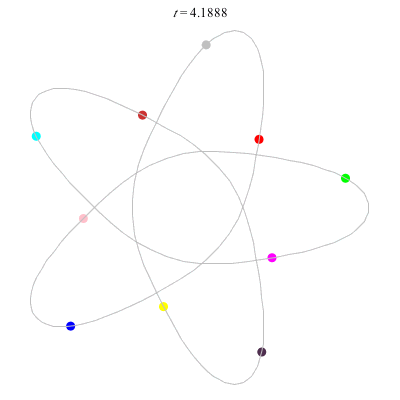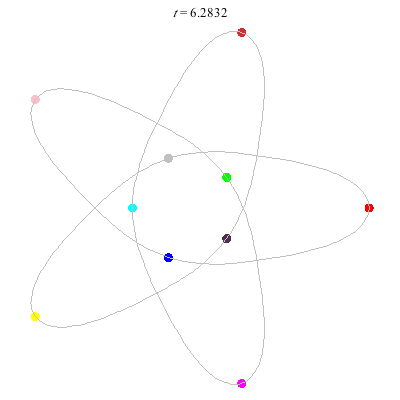
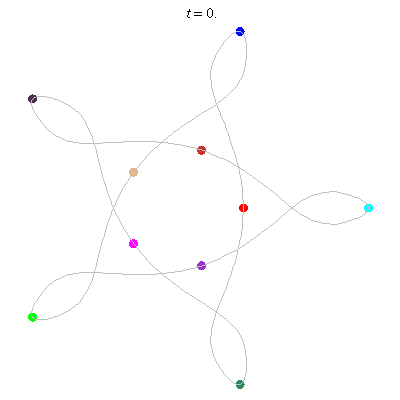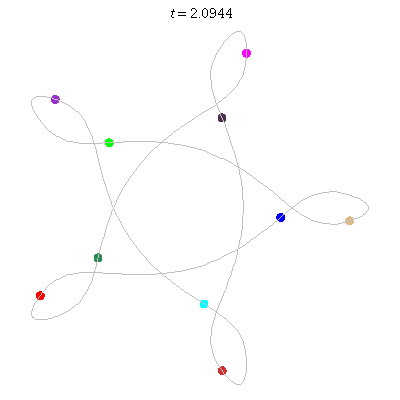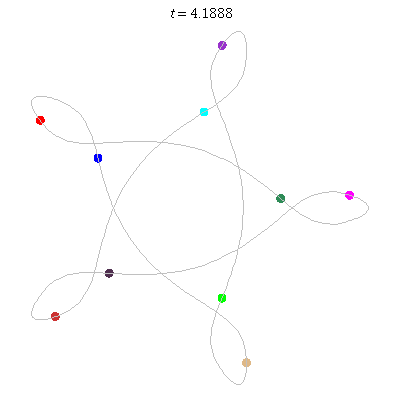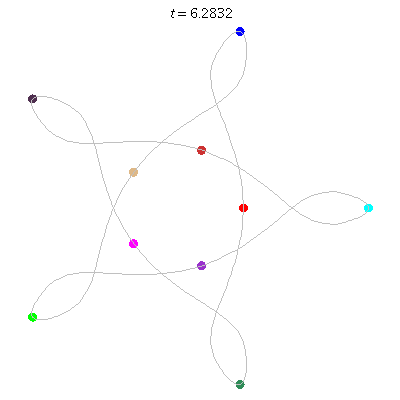
D(10,5/2)
- (a) Dancing pentagons
- action =
- winding nos = 2; -3, 2, 2, 2, -3.
- (b) balloons
- action =
- winding nos = -3; -3, -3, 2, -3, -3.
- (c) almost circular
- action =
- winding nos = -3; -3, -3, -8, -3, -3.
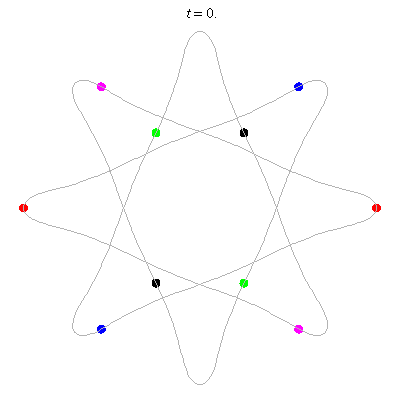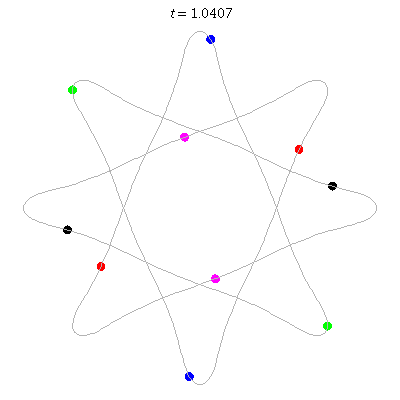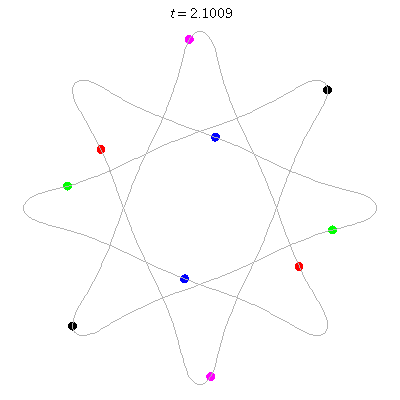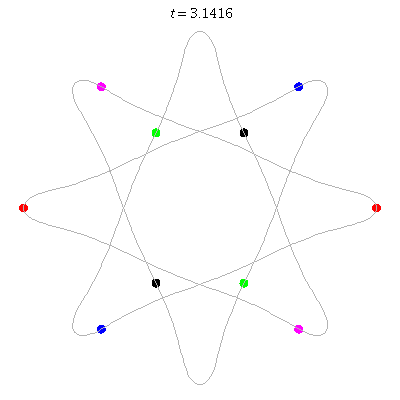
D(10,8/3)
- (a) 10 on an {8/3} octagram
- action =
- winding nos = ??.