These are choreographies with 2 curves
(and necessarily an even number of particles)
If the map between the two (oriented) curves is a rotation, we say they are corotating
if it is a reflection, we say it is counter-rotating.
If both, then non-oriented (?) (eg double figure 8 if it exists)
4 particles
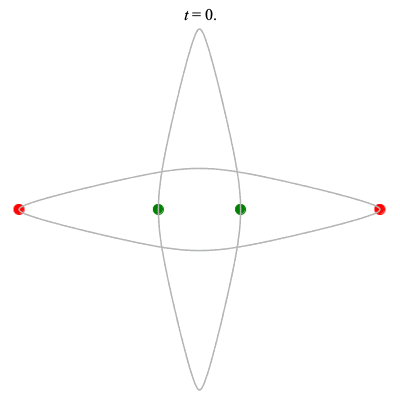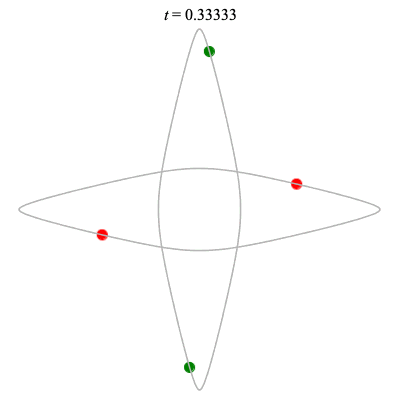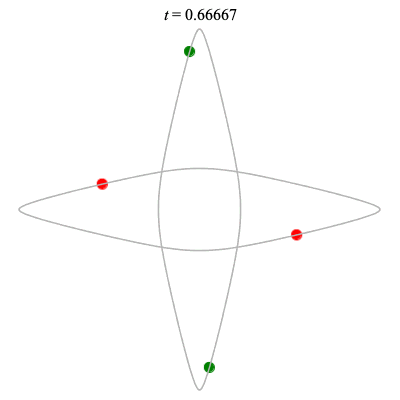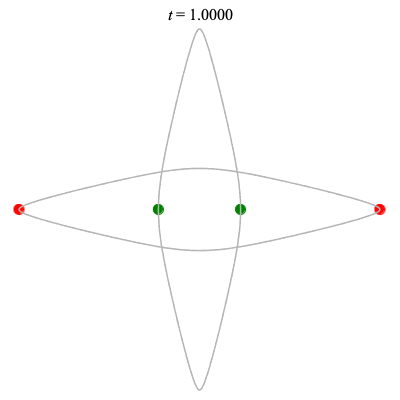
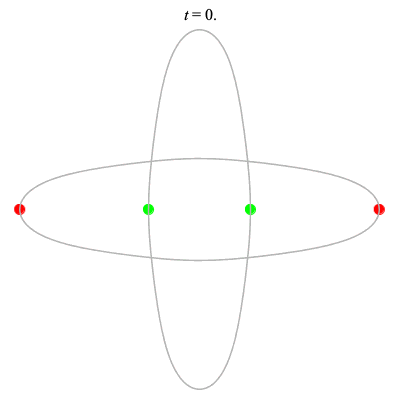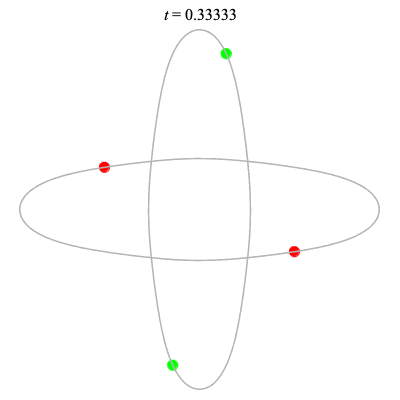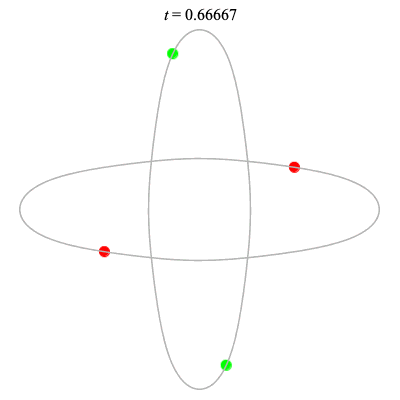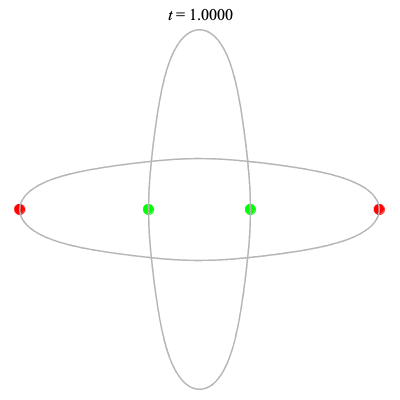
Dą(2x2,2) type
Corotating on left
Counter-rotating on right
(Core = \(C_2\))
The solution on the right was proved to exist by Chen (2001)
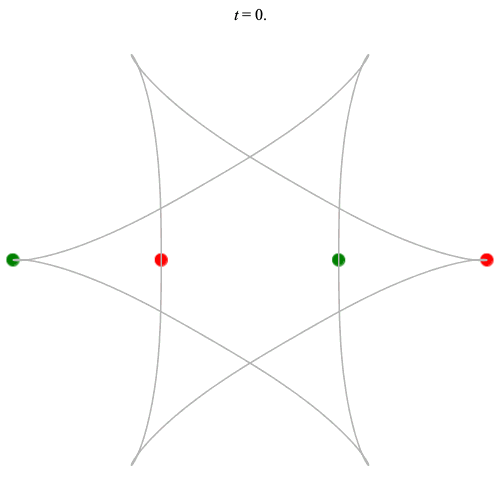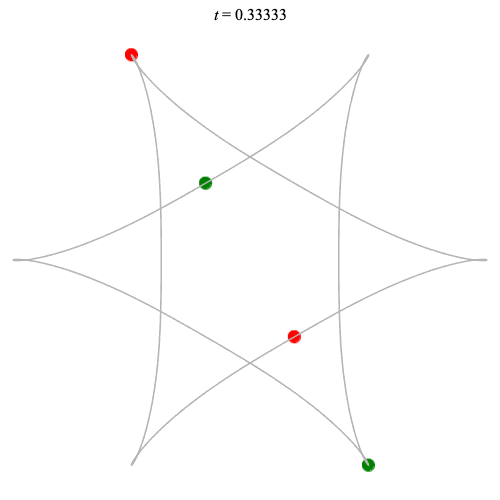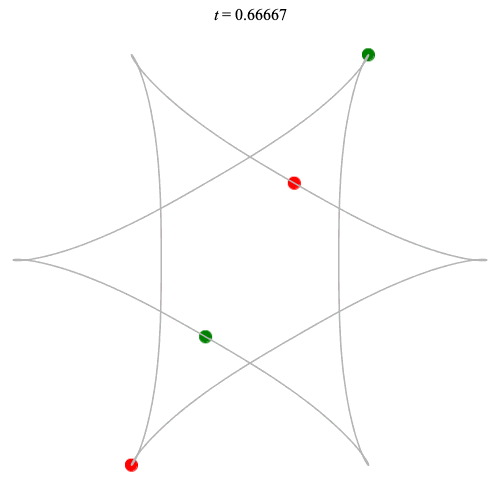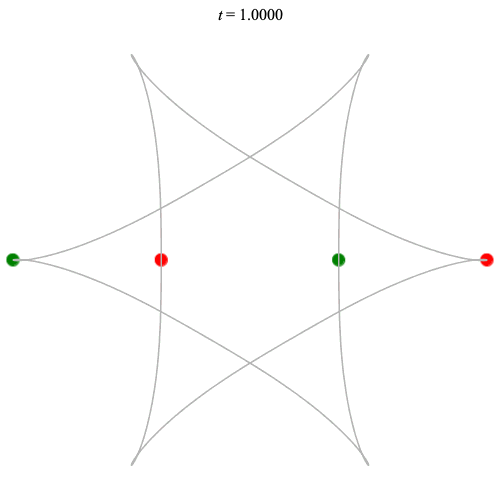
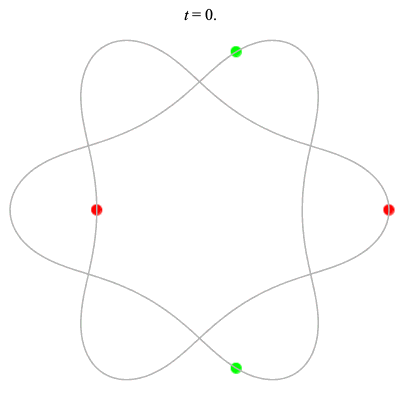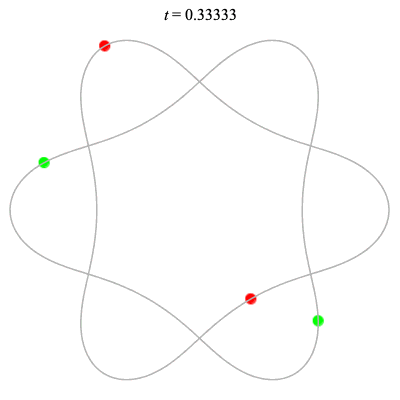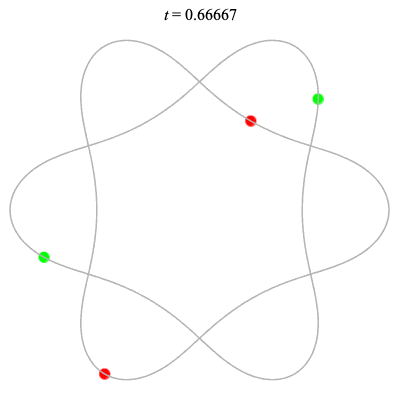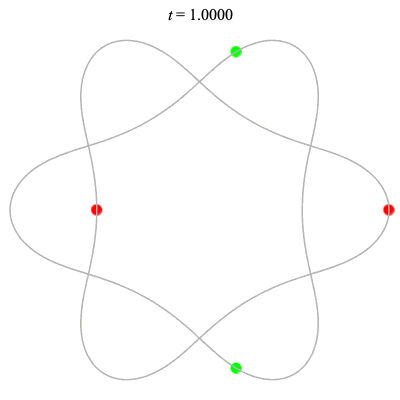
Dą(2x2,3) type
Corotating on left?
Counter-rotating on right
not convinced by one on right
The solution on the left was proved to exist by Chen (2003)
6 particles
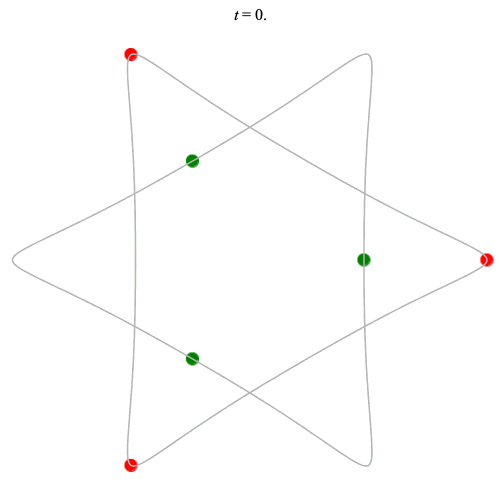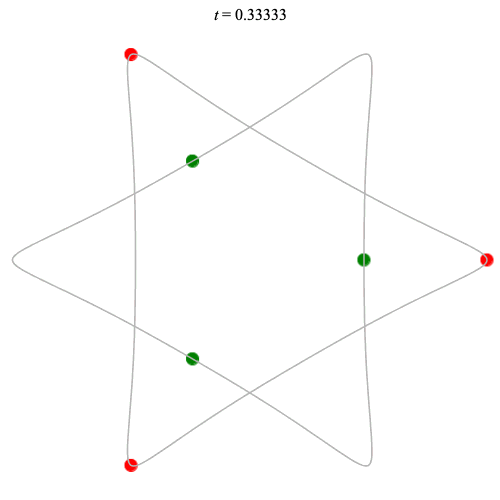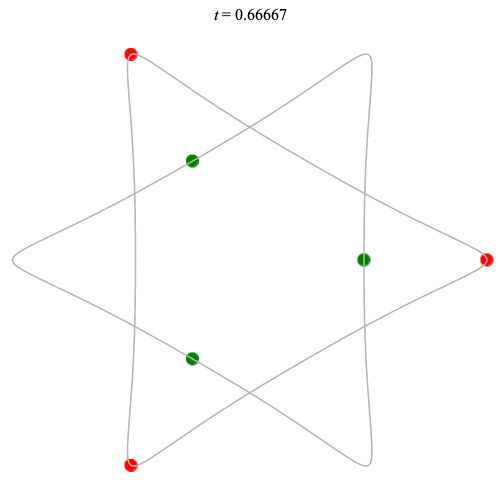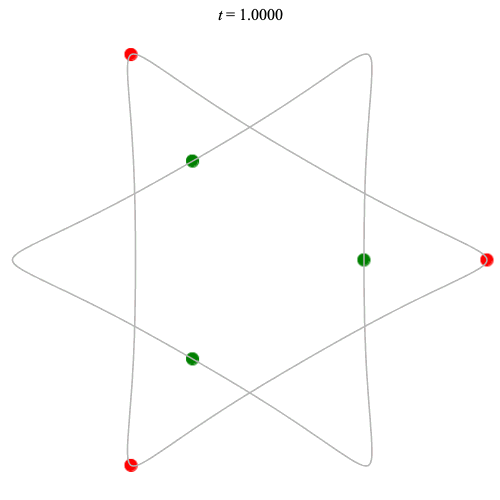
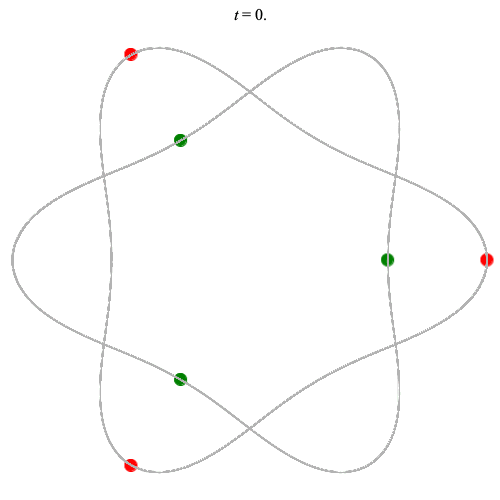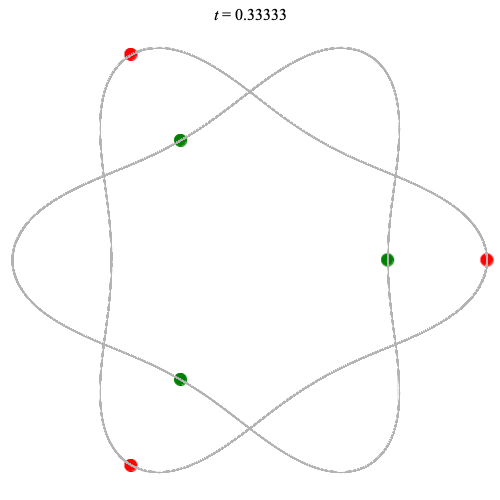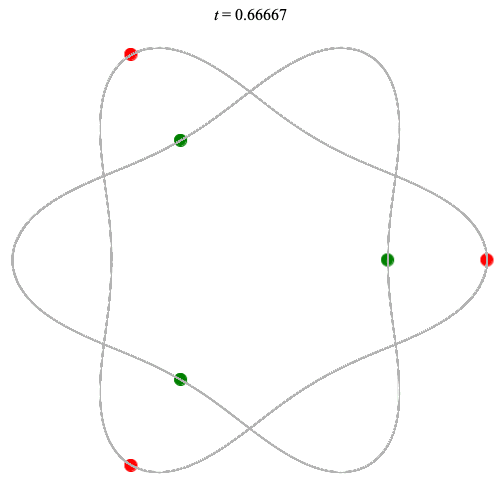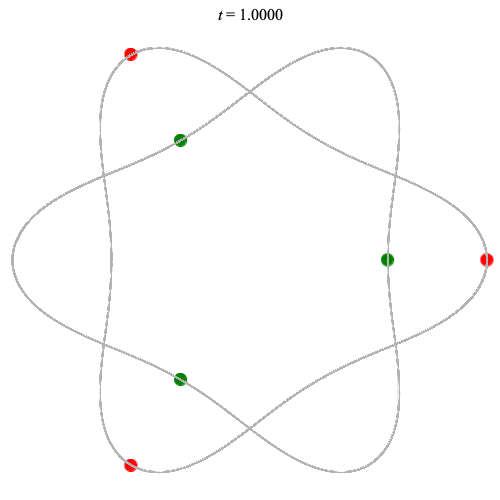
Dą(2x3,3) type
Corotating on left
Counter-rotating on right
(Core = \(C_3\))
(See also Chen (2003)?)
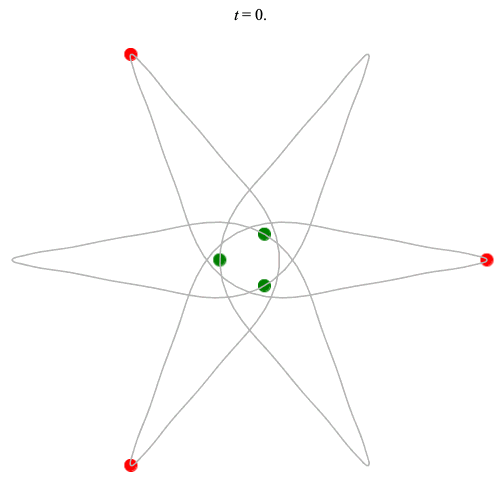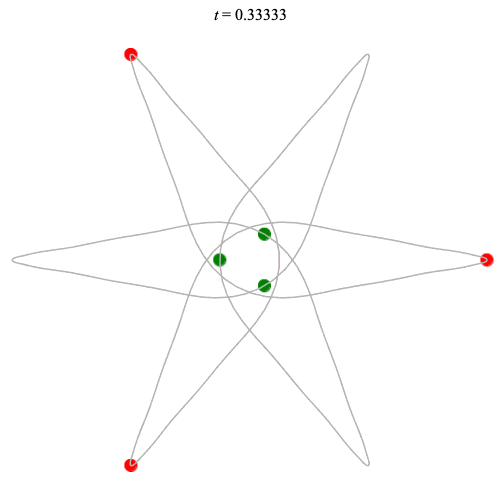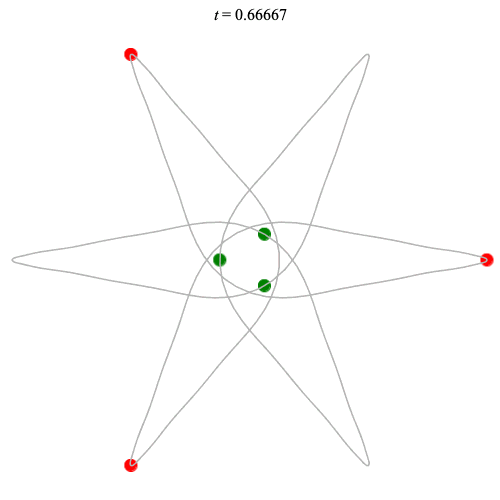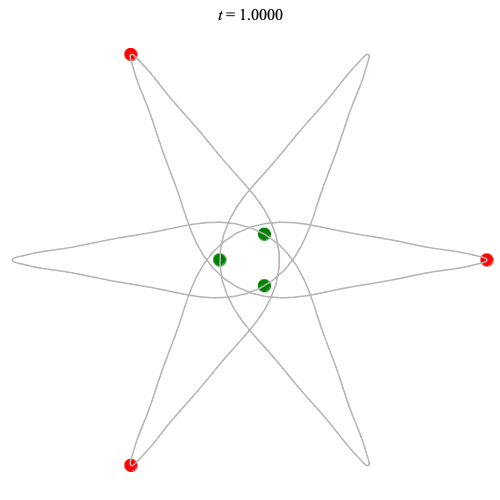
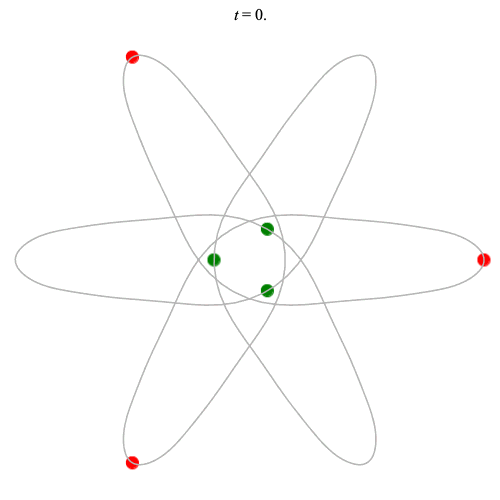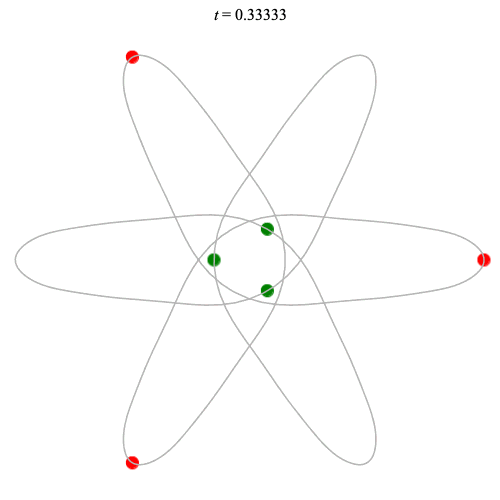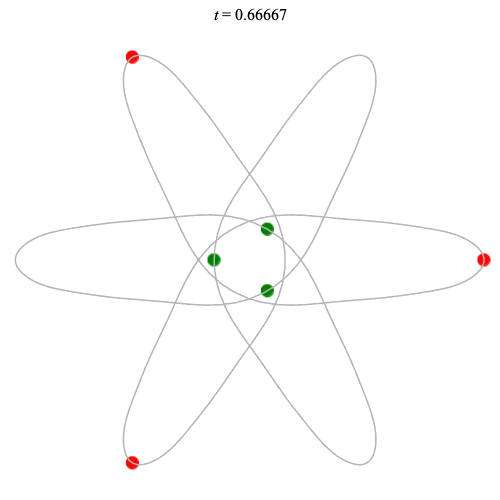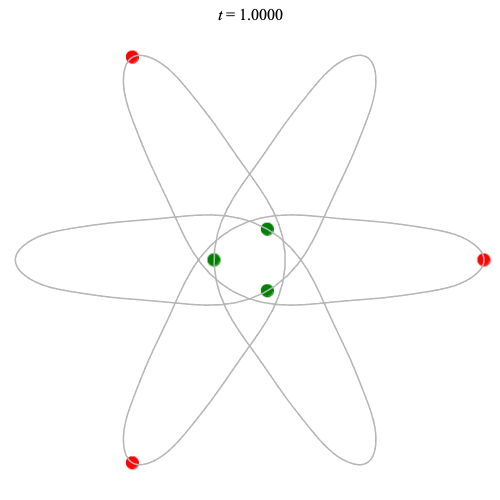
Dą(6,3/2) type
Corotating on left
Counter-rotating on right
(Core = \(C_3\))
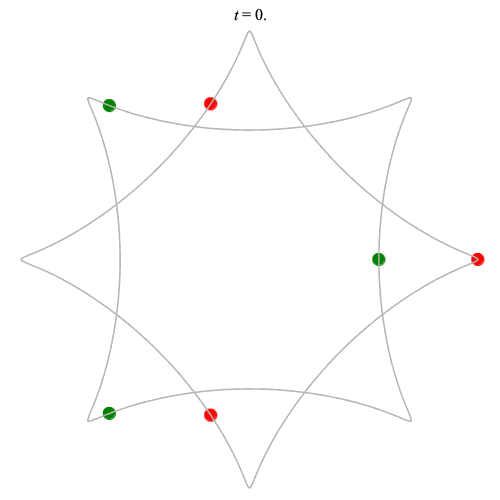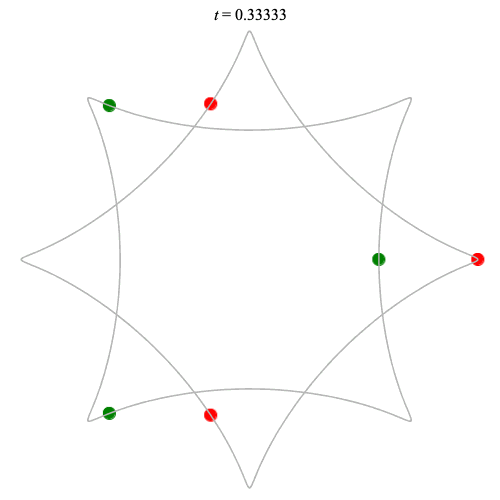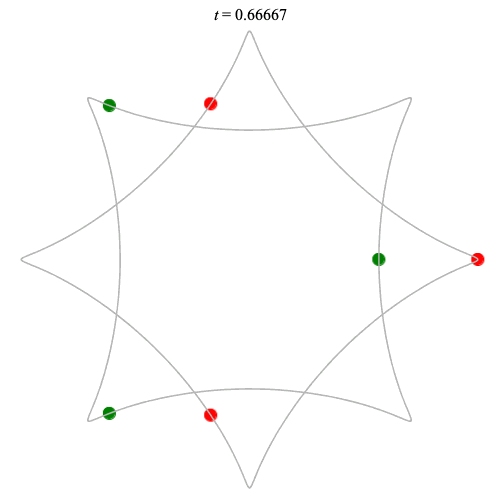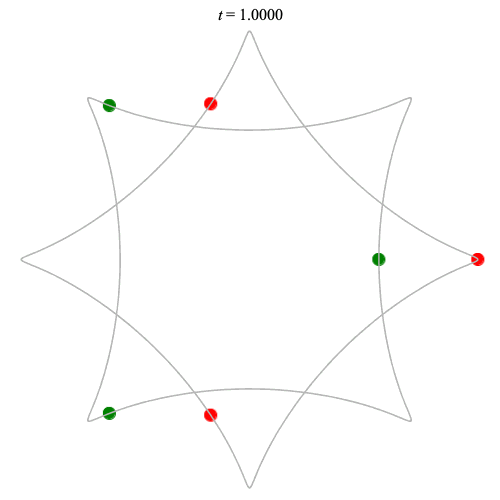
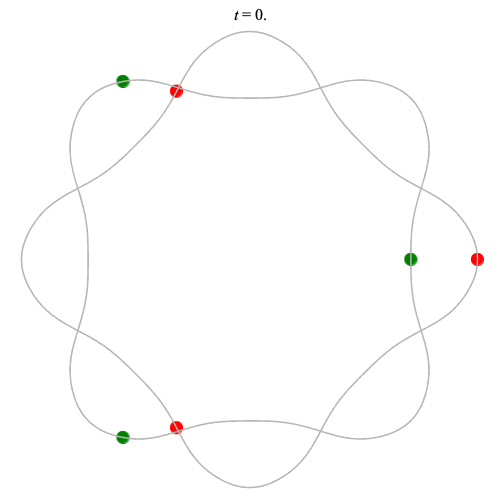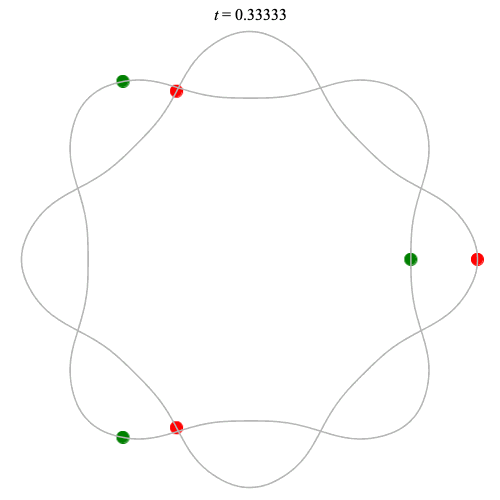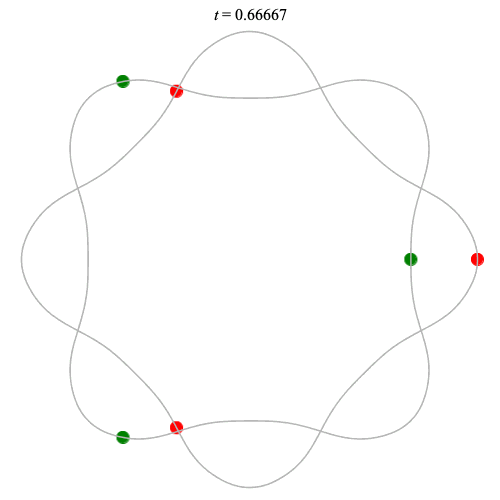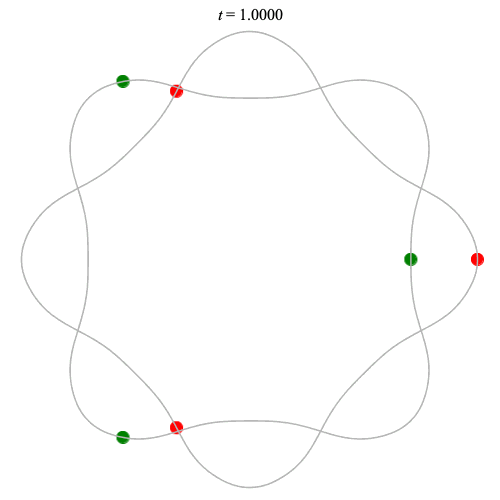
Dą(2x3,4) type
Corotating on left
Counter-rotating on right
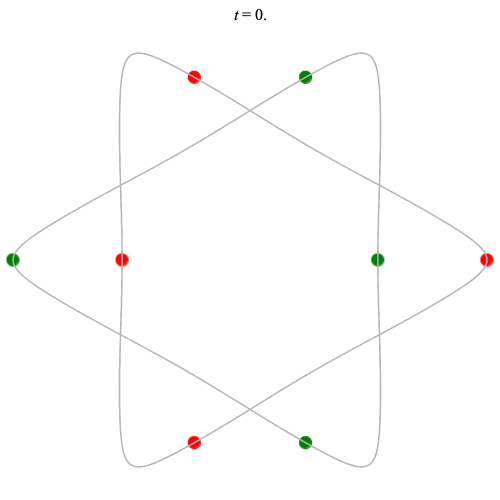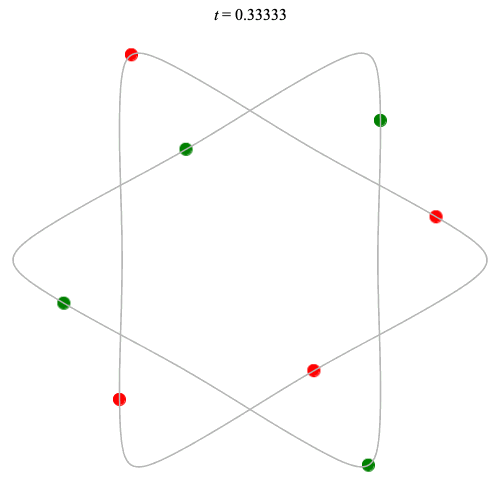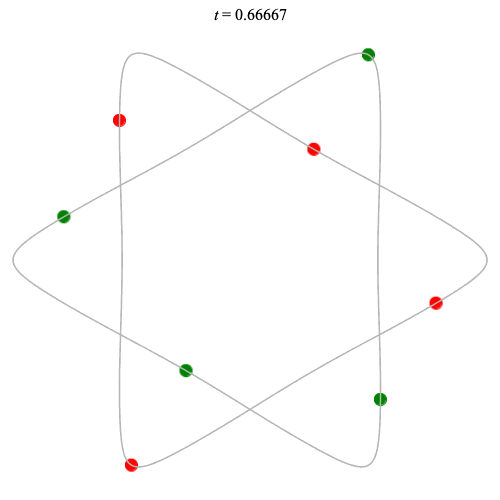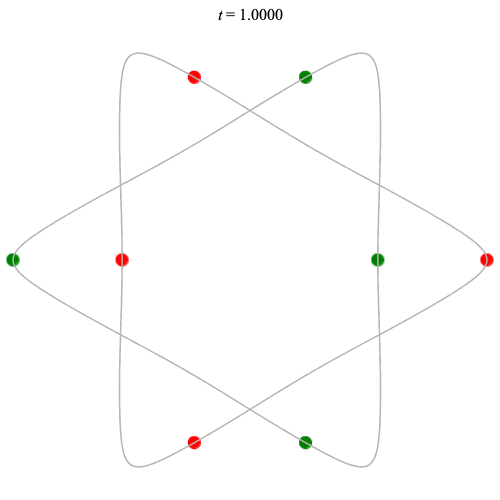
8 particles
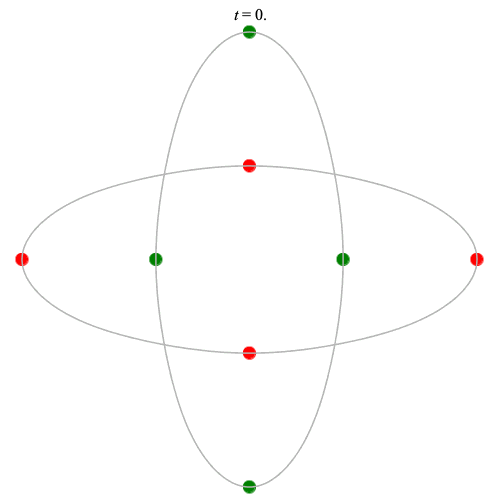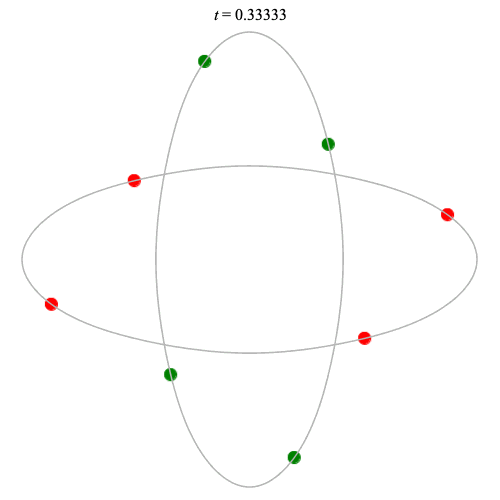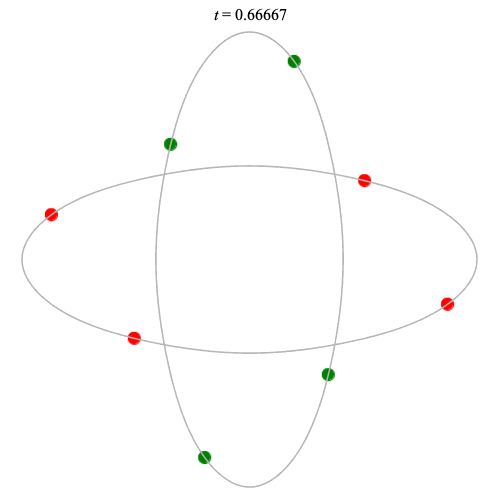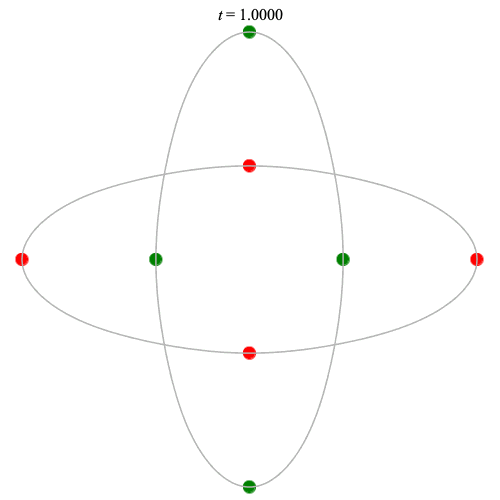
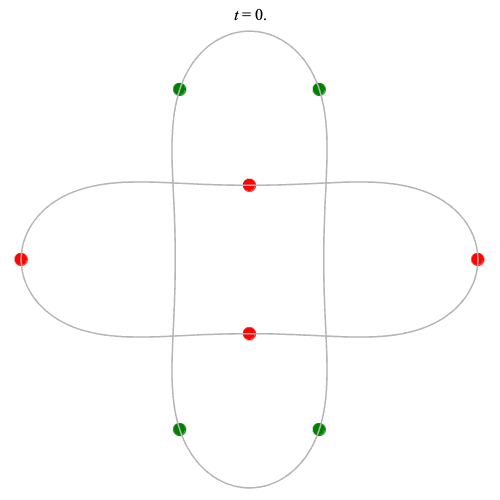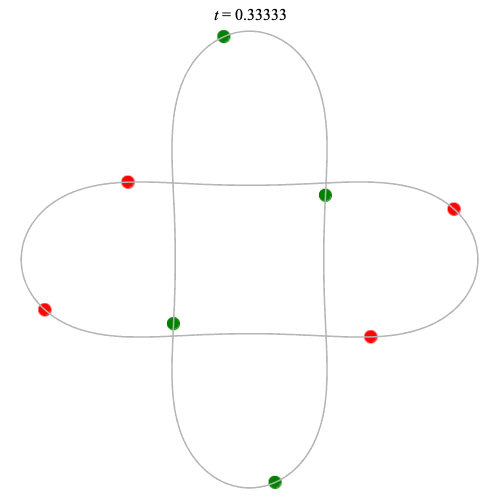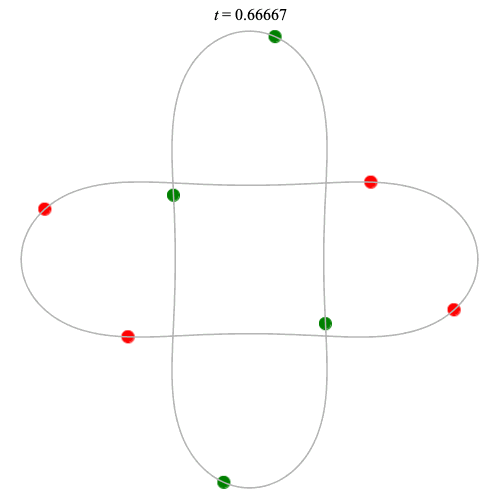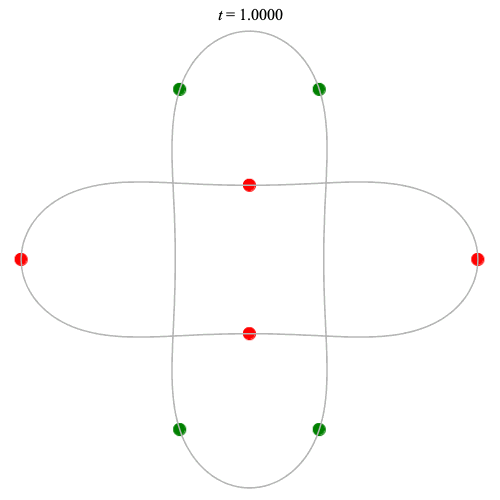
Dą(2x4,2) type
Corotating on left
Counter-rotating on right
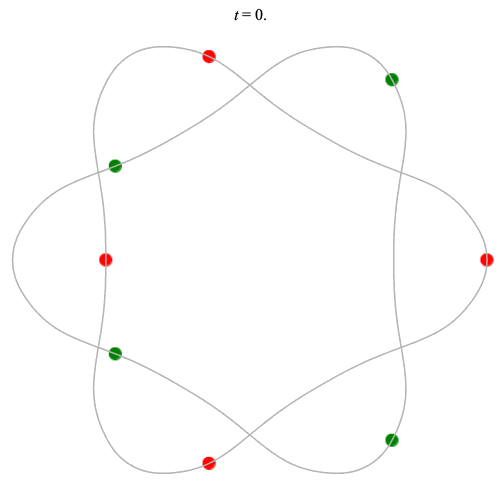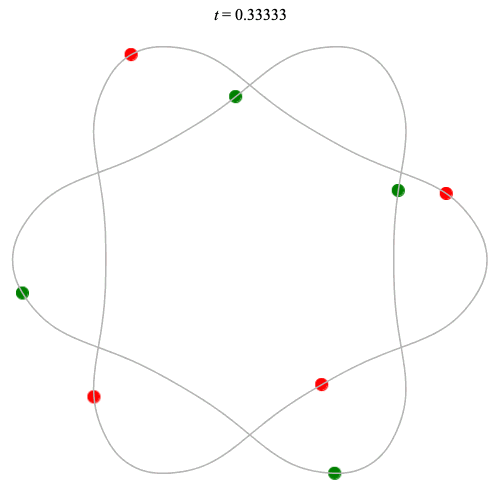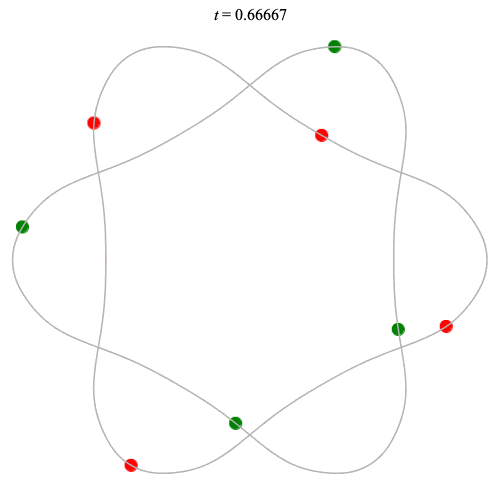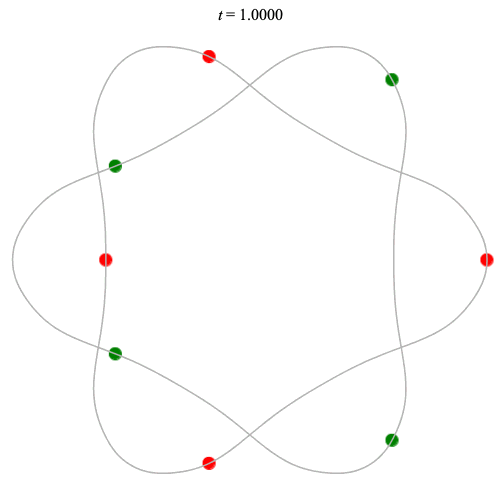
Dą(2x4,3) type
Corotating on left
Counter-rotating on right
(Not convnced by one on right)
8 particles - from Gerver's double-8
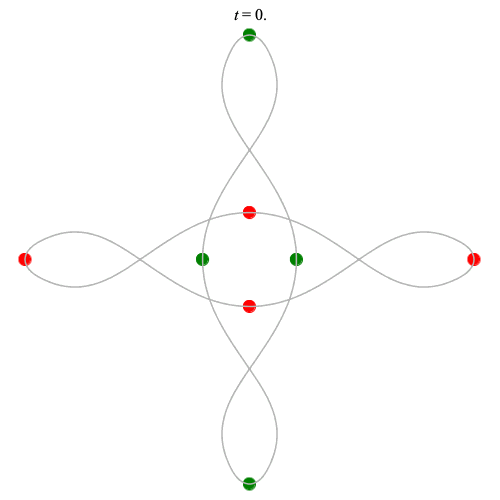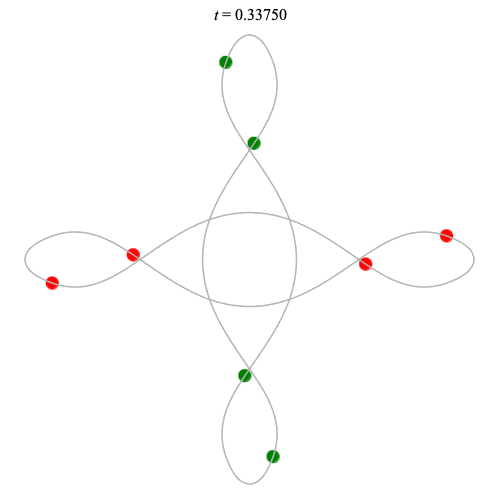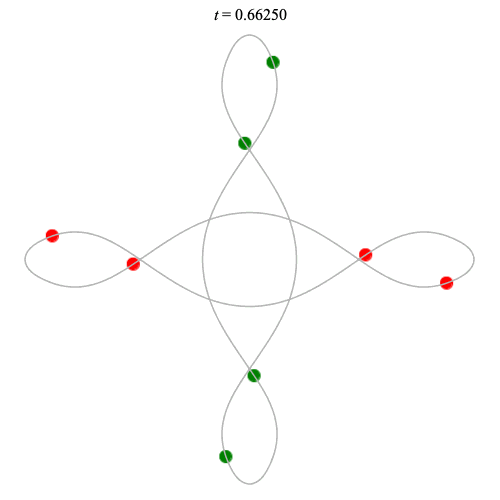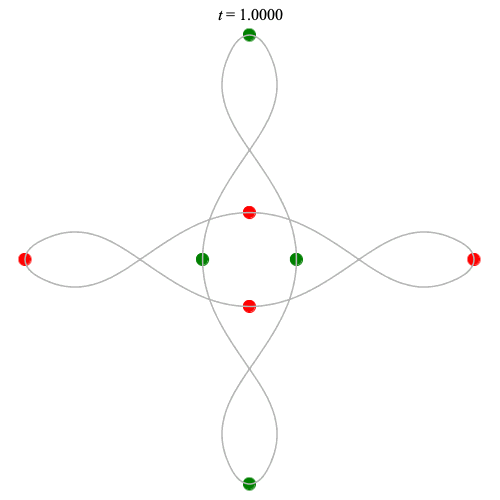Collision! if no time delay
D\(_+\)(2x4,2) type
Corotating on left
Counter-rotating on right
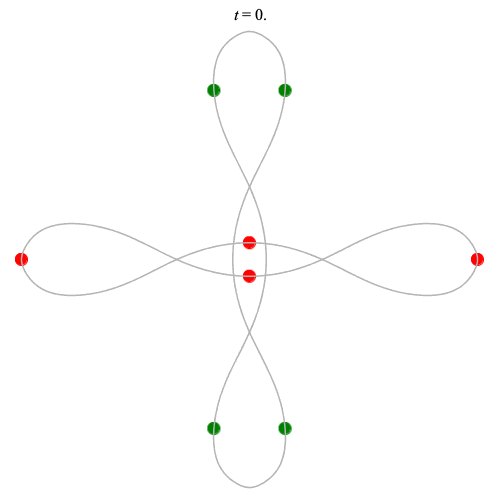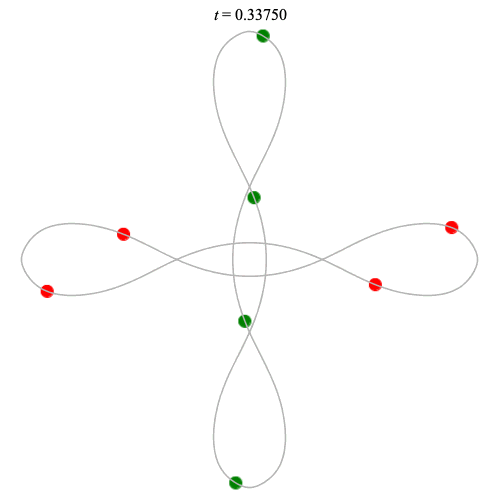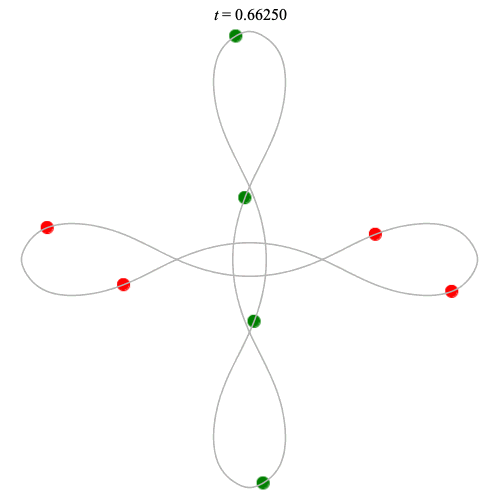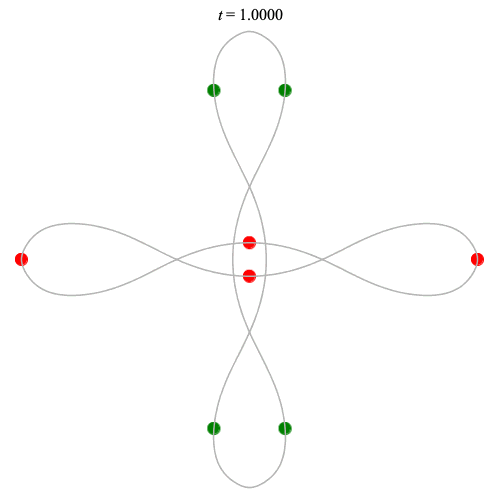
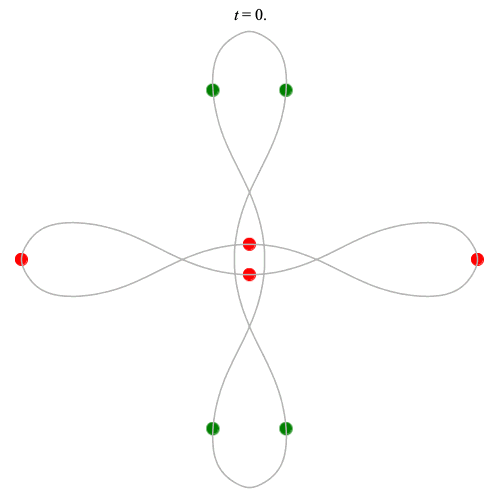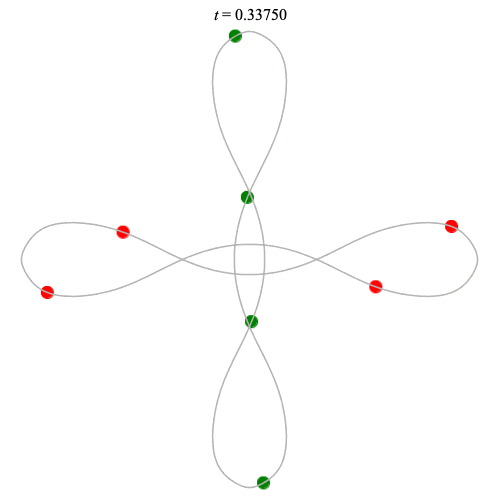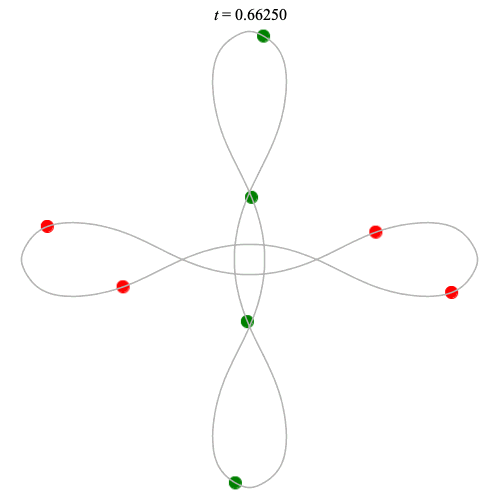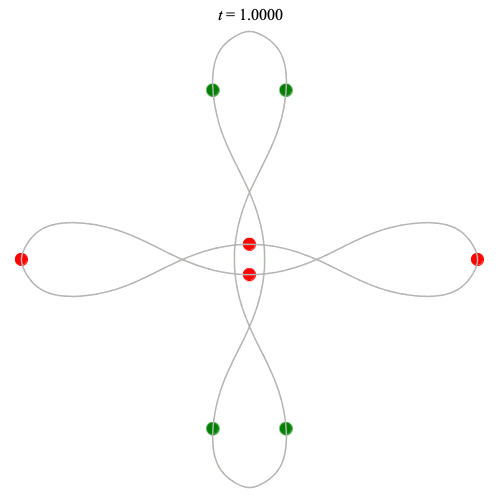
Dą(2x4,2) type
(with time delay)
Left: Corotating
Right: Counter-rotating
(curves are remarkably similar!)