The core is the set of symmetries existing for all values of time; that is, \(K=\ker\tau\). It is cyclic.

For the groups \(C(n,k/\ell)\) and \(D(n,k/\ell)\) the core is the cyclic group of order \((n,k)\).

D(6,4)

Core of order 2: the core symmetry involves rotation by \(\pi\) and the permutation \((1\;4)(2\;5)(3\;6)\).

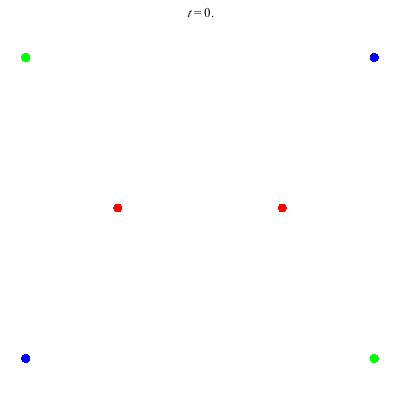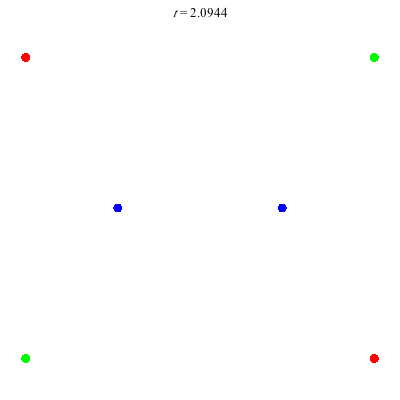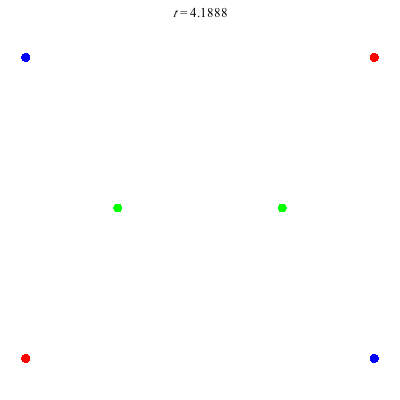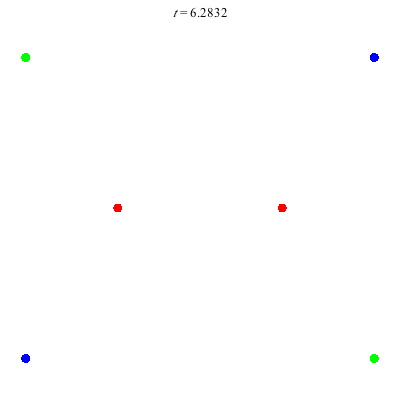
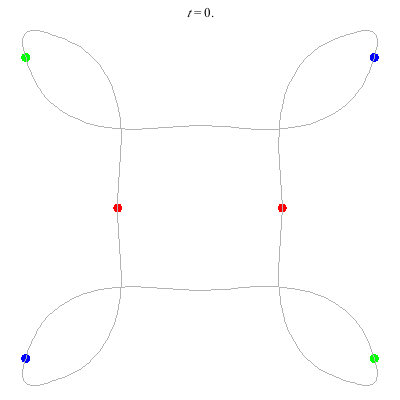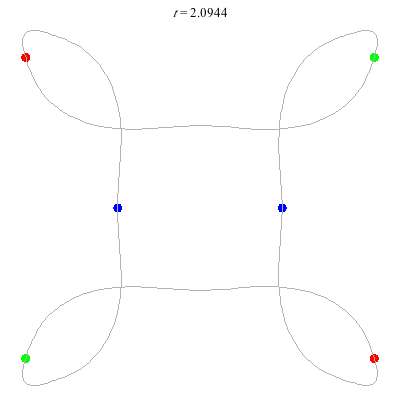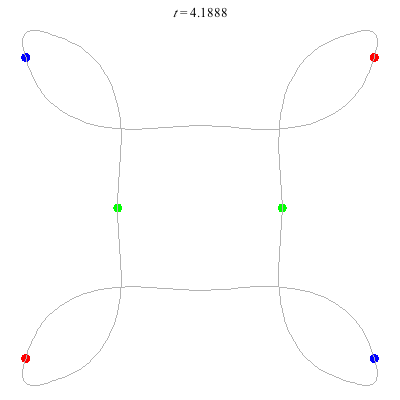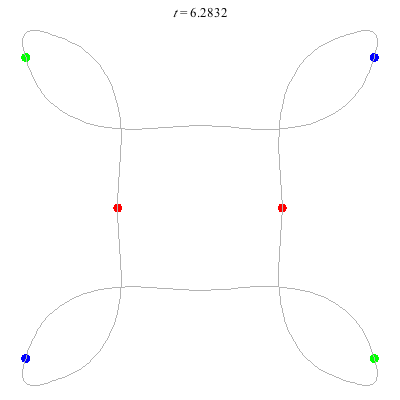
D(6,4)

D(8,4)

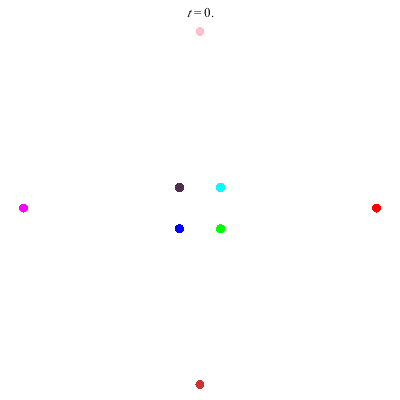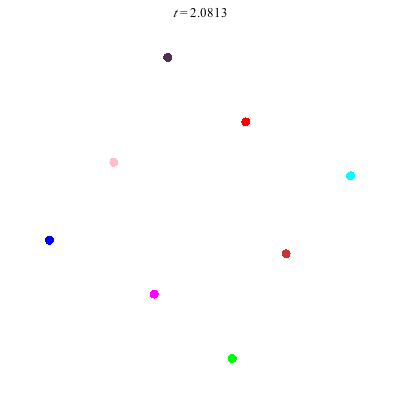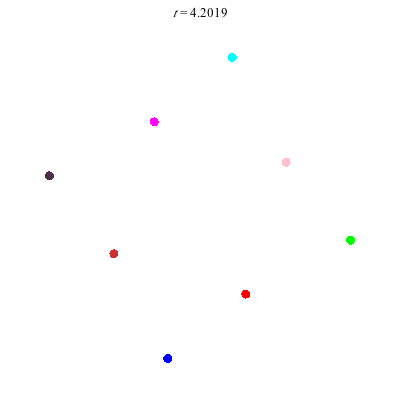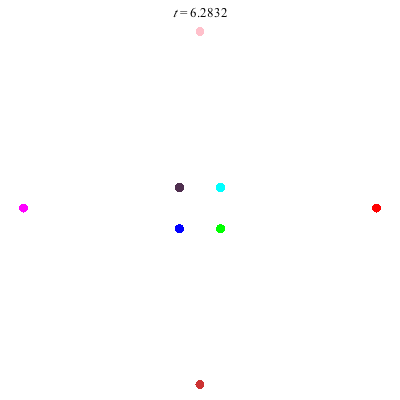
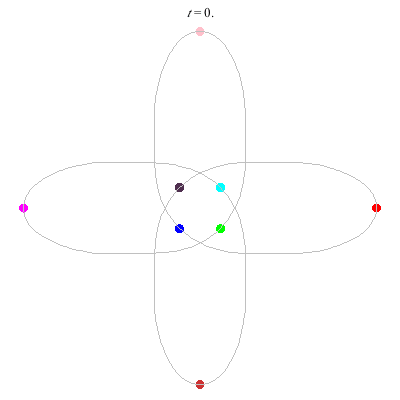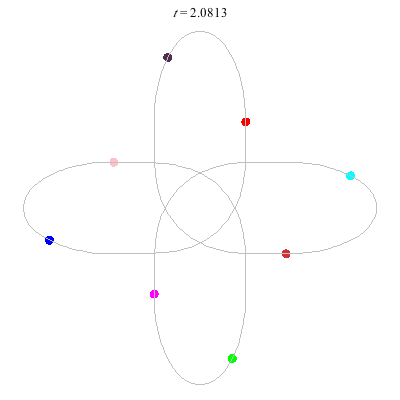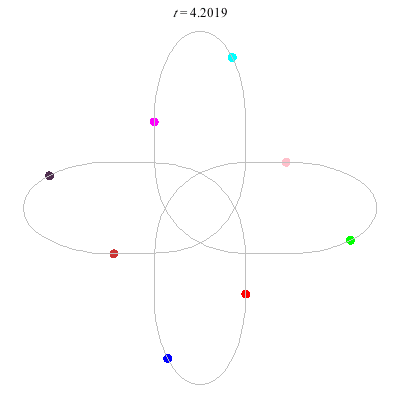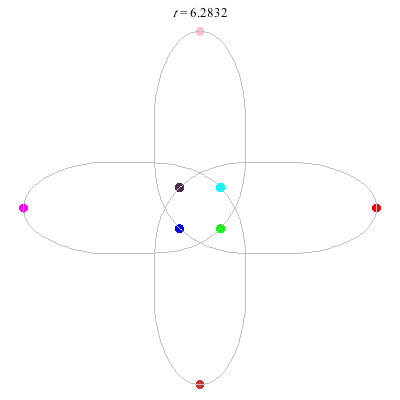
D(8,4) type
Newtonian force

D(4,6)

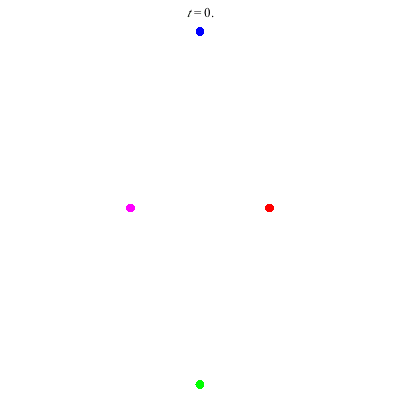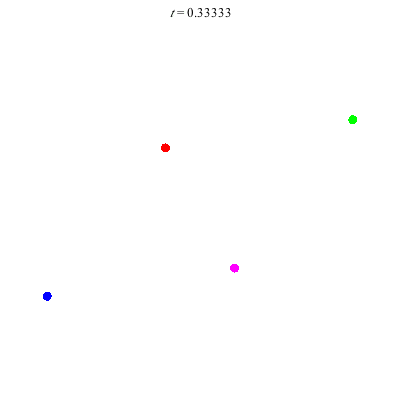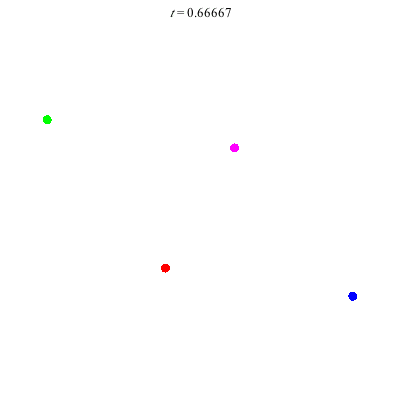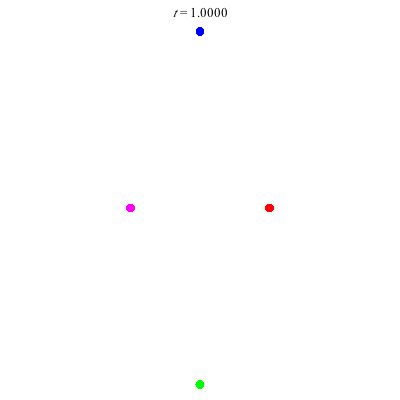
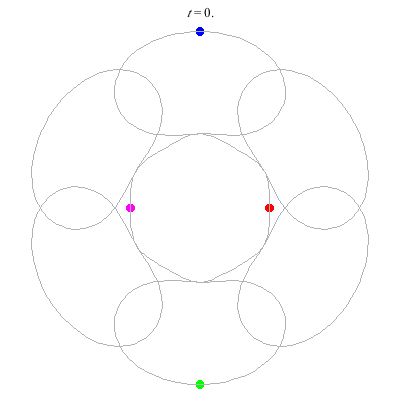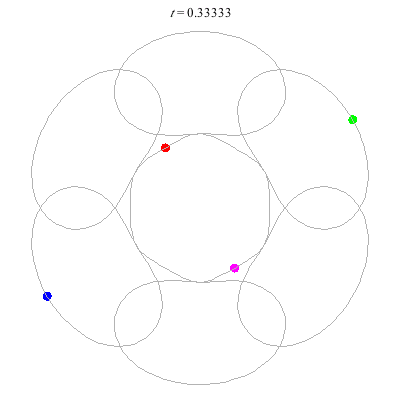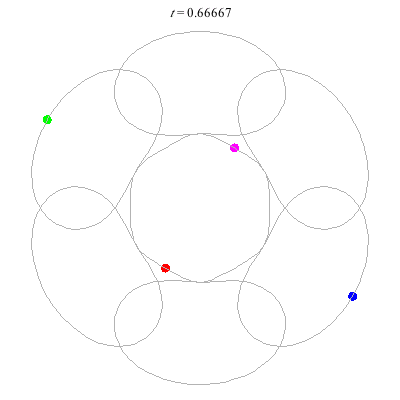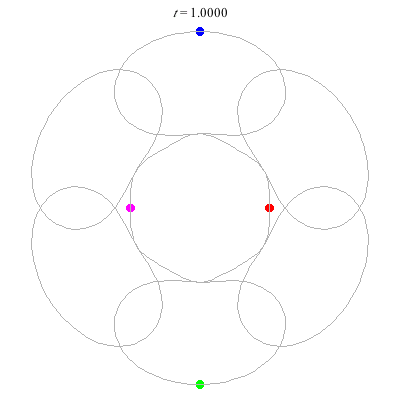
D(4,6) type
Newtonian force

D(10,5/\(\ell\))

These four pictures are of strong force choreographies with 10 particles, and 5-fold core (+ a reflectional symmetry).

The Fourier series are of the form \(\gamma(t) = \sum_r a_r \exp(2\pi i(5r+\ell)t).\) for appropriate values of \(\ell\)

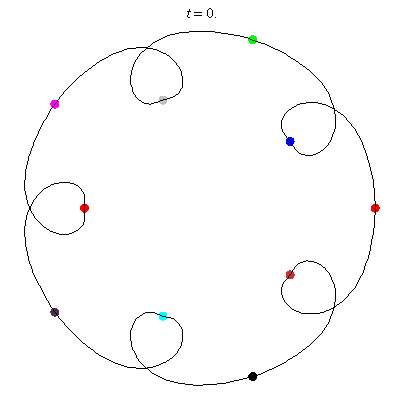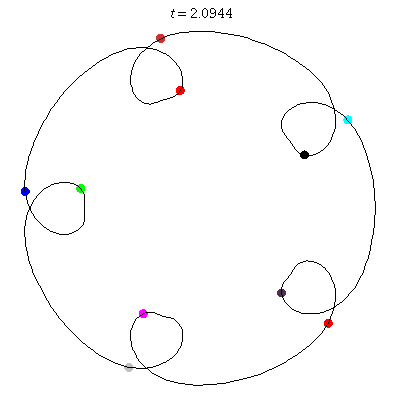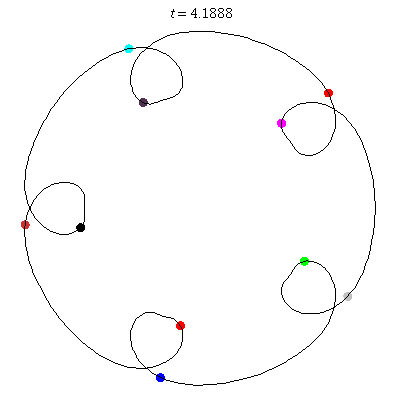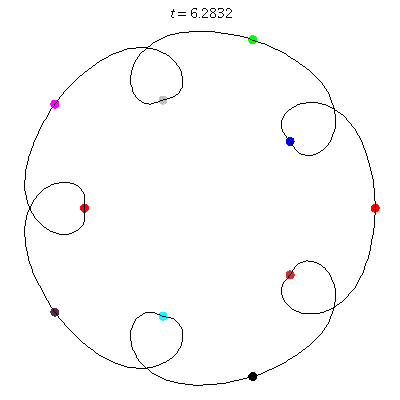
D(10,5)

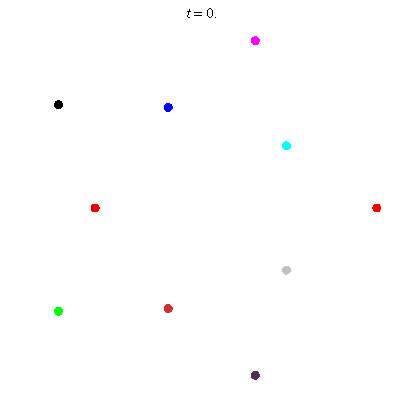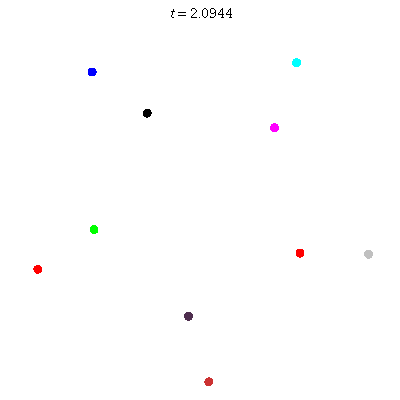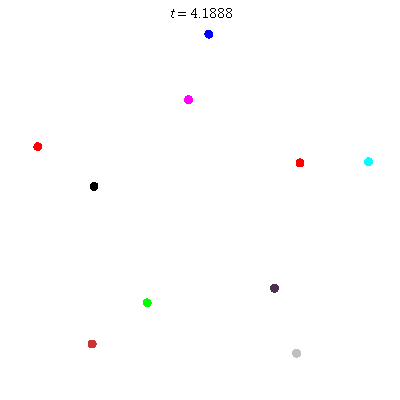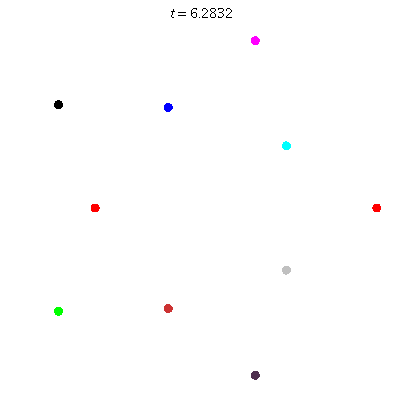
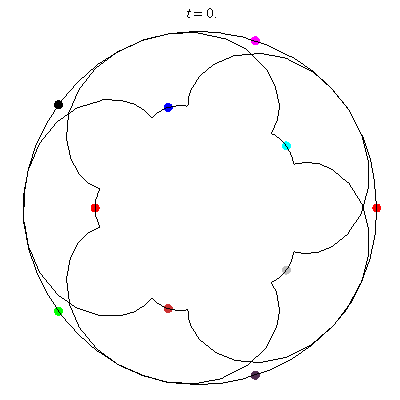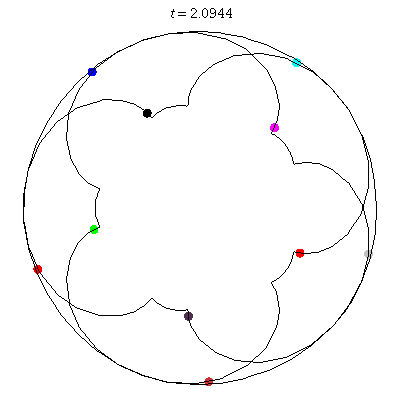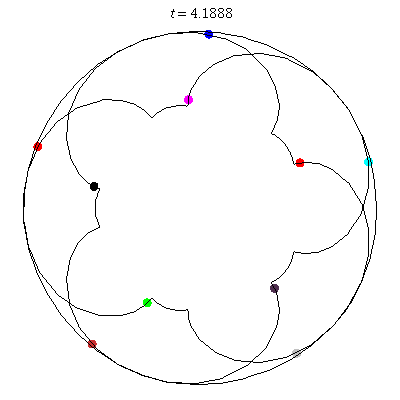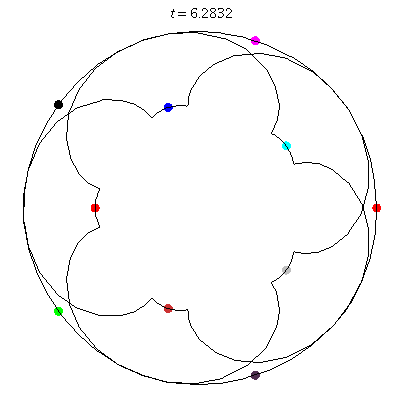
D(10,5/2)

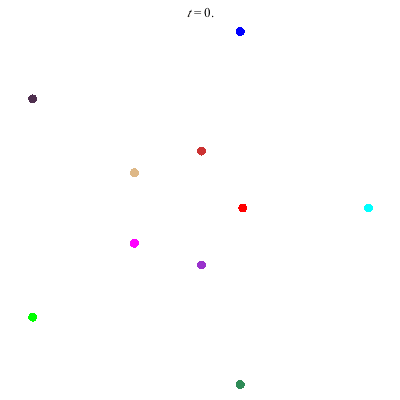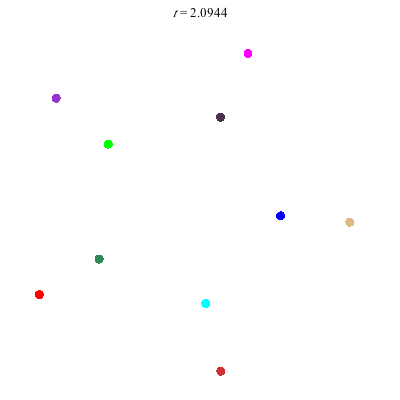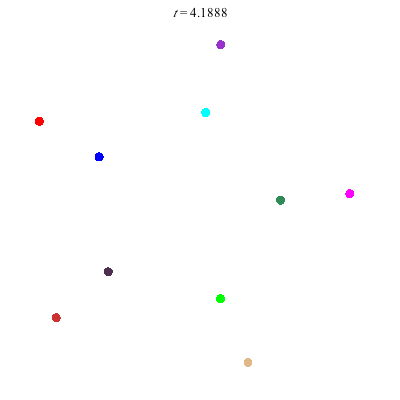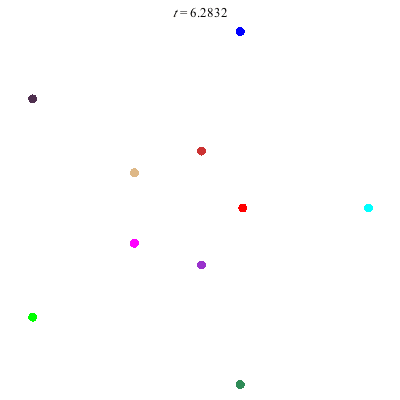
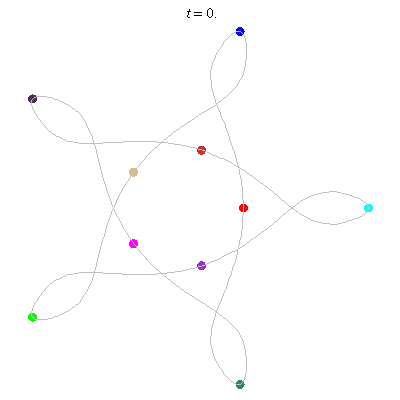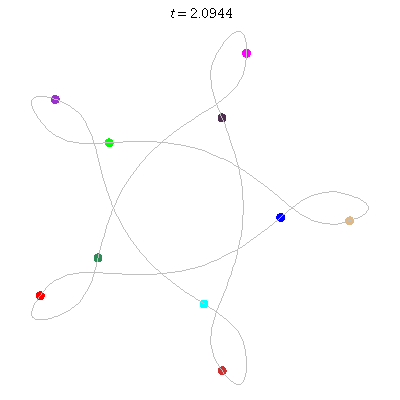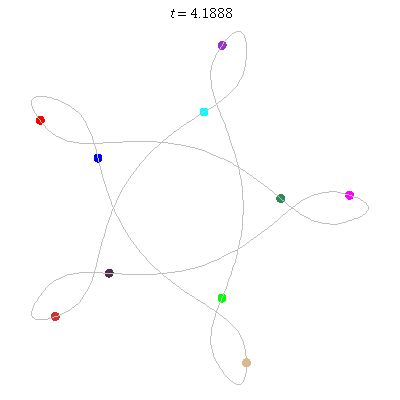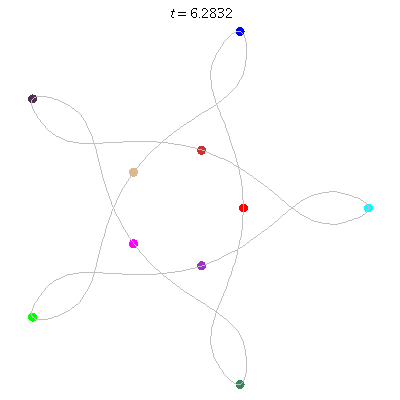
D(10,5/2)