Solutions
Problem 1
It follows from the queen's order that the ant-droids with numbers $$2^0 = 1, 2 =1, 2^2 = 4, 2^3 = 8, \ldots, 2^{17} = 131072$$ must be in pairwise distinct units as otherwise they would attack each other. This means that we need at least 18 different units.
Let us demonstrate that 18 units is enough. We create them as follows:
Unit 1: $1$.
Unit 2: $2,3$.
Unit 3: $4,5,6,7$.
...
Unit $k$: $2^{k-1},\ldots,2^k-1$.
...
Unit 18: $131072, \ldots, 250000$.
To see that this division suffices, let $x$ be any ant-droid in unit $k$. Then in particular $x \geq 2^{k-1}$ and hence for any $n \geq 2$, we have $nx \geq 2x \geq 2^{k}$, so no multiple of $x$ can be in unit $k$, therefore $x$ won't attack any ant-droid in its unit.
Answer: 18.
Problem 2
We will start with determining the probability of Jessie winning. Note that there are 90 2-digit numbers, with 9 of them containing zero, 9 having two equal digits, and 72 having different digits and not containing zero.
Assume that Jessie generated a number which contains zero, $\overline{a0}$ for some $a$ between $1$ and $9$. They win if Sasha has generated $\overline{aa}$ (1 outcome), $\overline{ba}$ for $b$ between $1$ and $9$ not equal to $a$ (8 outcomes), $\overline{ab}$ for $b$ between $1$ and $9$ not equal to $a$ (8 outcomes) or one of $10,20,\ldots,90$ (9 outcomes), that is in $1+8+8+9 = 26$ outcomes.
Assume that Jessie generated a number with same digits, $\overline{aa}$ for some $a$ between $1$ and $9$. They win if Sasha has generated $\overline{aa}$ (1 outcome), $\overline{ba}$ for $b$ between $1$ and $9$ not equal to $a$ (8 outcomes), $\overline{ab}$ for $b$ between $1$ and $9$ not equal to $a$ (8 outcomes) or $\overline{a0}$ (1 outcome), that is in $1+8+8+1 = 18$ outcomes.
Assume that Jessie generated a number with different non-zero digits,$\overline{ab}$ for some distinct $a,b$ between $1$ and $9$. They win if Sasha has generated $\overline{aa}$ or $\overline{bb}$ (2 outcomes), $\overline{ac}$ or $\overline{bc}$ for $c$ between $1$ and $9$ not equal to $a,b$ (14 outcomes), $\overline{ca}$ or $\overline{cb}$ for $c$ between $1$ and $9$ not equal to $a,b$ (14 outcomes), one of $\overline{ab}, \overline{ba}$ (2 outcomes) or one of $\overline{a0}, \overline{b0}$ (2 outcomes), that is in $2 + 14 + 14 + 2 + 2 = 34$ outcomes.
Thus, in total Jessie wins in $9 \cdot 26 + 9\cdot18 + 72\cdot34 = 2844$ outcomes out of $90\cdot 90 = 8100$ total outcomes. The game is fair if the weighted winnings for players are equal (equivalently, if the probability mean outcome for both is net zero), so if we denote probability of Jessie's victory by $p$ and their bet by $j$ (pounds), we must have equality $p \cdot 1 = (1-p) \cdot j$, meaning that $$j = \frac{p}{1-p} = \frac { \frac{2844}{8100} } {1 - \frac{2844}{8100} } = \frac{2844}{5256} \approx 0.5411.$$
Answer: $0.5411$.
Problem 3
Consider the hole drilled on the $x$-axis at some value $0 < k < 20$. The string tied at this hole has endpoints $(0,20-k)$ and $(k,0)$. Therefore it has slope $\frac{k-20}{k}$ and thus equation $y = \frac{k-20}{k}x + 20 - k = \frac{k-20}{k}(x-k)$.
Let $F(x)$ denote the function traced by the curve. The value of $F$ at a given point $x_0$ will be the highest possible value that is traced by a string at $x_0$, that is, highest possible value that $\frac{k-20}{k}(x_0-k)$ could take, varying $k$.
Let us maximize $\frac{k-20}{k}(x_0-k)$. This can be done by differentiation, but we show an elementary trick instead: this copies the usual proof of how the sum of a number and its reciprocal is always at least $2$. We begin by rewriting $$\frac{k-20}{k}(x_0-k)=x_0 + 20 -\frac{20x_0}{k} - k,$$ and since both $x_0$ and $k$ are positive, this expression is maximal when $k+\frac{20x_0}{k}$ is minimal. Notice that $$0 \leq (k-\sqrt{20x_0})^2=k^2-2k\sqrt{20x_0}+20x_0=k(k-2\sqrt{20x_0}+\frac{20x_0}{k}),$$ and since $k > 0$, this is equivalent to $k-2\sqrt{20x_0}+\frac{20x_0}{k} \geq 0$, that is, $k+\frac{20x_0}{k} \geq 2\sqrt{20x_0}$. Equality is attained by taking $k-\sqrt{20x_0}=0$.
It follows that the maximal possible value of $\frac{k-20}{k}(x_0-k)=x_0 + 20 -\frac{20x_0}{k} - k$ is $$x_0+20-2\sqrt{20x_0}=(\sqrt{x_0}-\sqrt{20})^2,$$ so the function $F$ is given by $F(x)=(\sqrt{x}-\sqrt{20})^2$. Substituting $x=\pi$, we get $(\sqrt\pi-\sqrt{20})^2\approx 7.2883.$
Answer: 7.2883.
Problem 4
We count the intersection points by distinguishing two cases: the two pairs of points determining the intersecting bisectors either have a point in common, or are $4$ distinct points.
First, note that for any three distinct points $A,B$ and $C$ on a plane, the perpendicular bisectors of $AB$, $BC$ and $CD$ are either all parallel (if the points are collinear) or intersect in a single point: the center of the circumcircle of the triangle formed by these three points. This contributes at most $\binom{100}{3} = 161 700$ intersection points.
Additionally, if we take four distinct points $A,B, C,D$, then assuming as long as all $6$ pairs formed from these points determine pairwise non-parallel lines, and the points $A,B, C,D$ do not lie on a circle, the perpendicular bisectors of $AB$ and $CD$, and of $AC$ and $BD$, and of $AD$ and $BC$ will intersect in $3$ distinct points. Therefore each quadruple contributes at most $3$ intersections, which is altogether at most $\binom{100}{4} \cdot 3=11763675$ intersection points.
It follows that the number of intersection points it at most $161 700+11763675=11925375$. We show that there is an arrangement of $100$ points achieving this upper bound.
We can construct such an arrangement inductively as follows. We begin by picking $3$ non-collinear points, and pick new points, one at a time, according to the following rules:
- for any pair of chosen points $A \neq B$, avoid picking a point on the line $AB$
- for any triple of pairwise distinct chosen points $A,B,C$, avoid picking a point on the circumcircle of $ABC$
- for any triple of pairwise distinct chosen points $A,B,C$, avoid picking a point on the line which passes through $A$ and is parallel to $BC$
- for any pairs of chosen points $A \neq B$ and $C \neq D$, denoting the perpendicular bisectors of $AB$ and $CS$ by $p_{AB}$ and $p_{CD}$ respectively, avoid picking a point on the circle with center $p_{AB} \cap p_{CD}$, passing through a chosen point $E$.
Note that we only have finitely many circles and lines excluded in each step, so there are always points on the plane still available to pick from.
We now show that if we chose $100$ points according to the rules above, all intersections we counted exist, and all intersections we counted as distinct are distinct. That is, if an intersection point has $3$ distinct bisectors passing through it, those $3$ bisectors are determined by $3$ points.
To see that all intersections exist, observe that the bisectors of $AB$ and $CD$ are parallel if and only if $AB$ is parallel to $CD$ (note: we do not assume here that $A,B,C,D$ are pairwise distinct, but we have $A \neq B, C \neq D$ and $\{A,B\} \neq \{C,D\}$). However, if we had such points $A,B,C,D$, then the last point chosen among $A,B,C,D$ would have violated rule (i) or (iii).
For the statement about distinctness, assume for contradiction that a point $P$ on the plane has $3$ distinct bisectors $p_{AB}$, $p_{CD}$ and $p_{EF}$ passing through it, corresponding to the pairs $A,B$; $C,D$, and $E,F$, where $\{A,B,C,D,E,F\}\geq 4$. Suppose that $F$ was chosen last among $\{A,B,C,D,E,F\}$. Notice that $F$ lies on the circle with center $P=p_{AB} \cap p_{CD}$ passing through the point $E$. If $F \notin \{A,B,C,D,E\}$, then the choice of $F$ must have violated rule (iv). Otherwise, if $F \in \{A,B,C,D,E\}$, for example, $F=A$, then $P$ ic the center of he circumcircle of $BFE$, so the bisector $p_{EB}$ also passes through $P$, and in particular $p_{EB} \cap p_{CD}=P$. If $F \notin \{B,C,D,E\}$, then again its choice violated role (iv). If $F \in \{B,C,D,E\}$, say $F=C$ (note: $F \neq B, E$ by assumption), then $P=p_{FB} \cap p_{FD} \cap p_{EF}$, which implies that $P$ is of equal distance from all four points $B,D,E,F$, therefore they lie on a circle. We have $F \notin \{B,D,E\}$ by the assumption that $\{A,B,C,D,E,F\}\geq 4$. So the choice of $F$ violated the rule (ii).
We have thus shown that if a point $P$ has $3$ distinct bisectors $p_{AB}$, $p_{CD}$ and $p_{EF}$ passing through it, then $\{A,B,C,D,E,F\}=3$, and $P$ is the center of the circle determined by these $3$ points. It also follows that no point has $4$ or more bisectors passing through it: if it did, we would find that $3$ of these bisectors violate the previous condition. This shows that all intersections we counted as distinct are indeed distinct.
An example for an optimal selection of $5$ points is illustrated below. There are $\binom{5}{3}=10$ points in which exactly $3$ bisectors intersect (coloured orange), and $\binom{5}{4} \cdot 3=15$ points in which exactly $2$ bisectors intersect (coloured green).
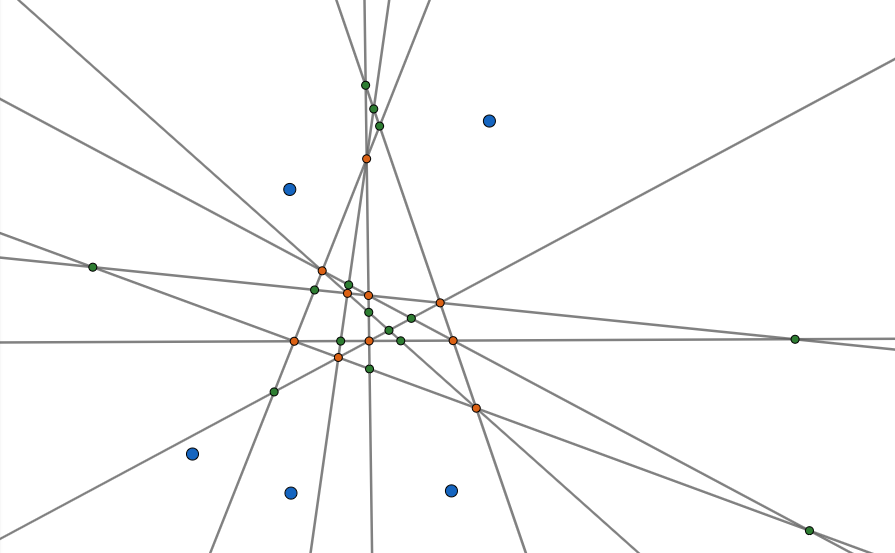
Answer: $11925375$.
Problem 5
In order to explain the solution let us represent the holes on pegboard in the Cartesian coordinate system, starting with $(0,0)$ at the left lower corner, going up to $(4,4)$ in the right upper corner, with the axes parallel to the sides of the board.
Assume that the initial peg is glued in $(0,0)$, and denote the coordinates of the other pegs by $(a,b)$ and $(c,d)$ with $0 \le a,b,c,d \le 4$. By Pythagorean theorem, the squares of the length of the segments $(0,0) (a,b)$, $(0,0) (c,d)$ and $(a,b) (c,d)$ are $a^2+b^2$, $c^2 + d^2$ and $(a-c)^2 + (b-d)^2$ respectively.
If the right angle is at $(0,0)$, then $(a,b) (c,d)$ is the hypotenuse and we have $(a^2+b^2) + (c^2 + d^2) = (a-c)^2 + (b-d)^2$. Simplifying this expression we get $ac+bd = 0$. Since $a,b,c,d \ge 0$, either $ac >0$ or $bd > 0$ would imply $ac+bd > 0$, so in order to find a solution, we need $ac = 0$ and $bd = 0$. The former implies that either $a$ or $c$ is zero: if $a$ is zero, $b$ cannot be zero (pegs are distinct), so $d$ is zero. Similarly, if $c$ is zero, $b$ is zero. This means that the other two pegs must be placed along the left and bottom side of the pegboard, resulting in $4 \cdot 4 = 16$ triangles.
If the right angle is not at $(0,0)$, assume it is at the vertex $(a,b)$. By the Pythagorean theorem, we obtain the equality $(a^2+b^2)+((a-c)^2 + (b-d)^2) = c^2 + d^2$, which can be simplified into $a^2 + b^2 = ac + bd$, or equivalently $a(a-c) = b(d-b)$. There are two distinct possibilities: either both sides are zero, or both are nonzero.
If $a(a-c) = 0$ and $b(d-b) = 0$ there are the following subcases.
- $a=0,b=0$ -- impossible due to pegs being distinct
- $a-c = 0, d-b = 0$ or $a=c,b=d$ -- impossible due to pegs being distinct
- $a=0, d=b$ -- 16 triangles ($c$ can be anything between $0$ and $4$ except for zero since the pegs are different, which gives us 4 option and $b=d$ can be anything between $0$ and $4$ except for zero for the same reason, giving us 4 more options)
- $a-c =0, b =0$ -- 16 triangles ($d$ can be anything between $0$ and $4$ except for zero since the pegs are different, which gives us 4 option and $a=c$ can be anything between $0$ and $4$ except for zero for the same reason, giving us 4 more options)
If $a(a-c) \neq 0$ and $b(d-b) \neq 0$, we have $a \neq 0$ and $b \neq 0$. Note that $a-c$ and $d-b$ are either both positive or both negative. If $a < c$, we can flip the pegboard across diagonal $x=y$, resulting in a triangle with coordinates $(b,a)$ and $(d,c)$ with $b>d$. Thus, we can limit ourselves to the case $a>c$ and then multiply the number of triangles counted by $2$. Remember that $1 \le b,d \le 4$.
- $a=1, c=0$. We get $1 = b (d-b)$, which means $b= 1, d-b=1$, i.e. $d=2$ (1 triangle);
- $a=2, c= 0$. We get $4 = b(d-b)$, which means $b=1, d- b = 4$,i.e $d=5$ (impossible), $b=2, d-b=2$, i.e. $d=4$ or $b=4, d-b=1$, i.e. $d=5$ (impossible, 1 triangle in total);
- $a=2, c=1$. We get $2 = b (d-b)$, which means $b=2, d-b =1$, i.e. $d=3$, or $b=2, d-b =1$, i.e. $d=3$ (2 triangles);
- $a=3, c=0$. We get $9 = b (d-b)$, which means $b=3, d-b =3$, i.e. $d=6$ (impossible), or $b=1, d-b =9$, i.e. $d=10$ (impossible, no triangles);
- $a=3, c=1$. We get $6= b(d-b)$, which means $b=3, d-b =2$, i.e. $d=5$ (impossible), $b=2, d-b =3$, i.e. $d=5$ (impossible), or $b=1, d-b =6$, i.e. $d=7$ (impossible, no triangles);
- $a=3, c=2$. We get $2 = b (d-b)$, which means $b=3, d-b =1$, i.e. $d=4$, or $b=3, d-b =1$, i.e. $d=4$ (2 triangles);
- $a=4, c=0$. We get $16= b(d-b)$, which means $b=4, d-b =4$, i.e. $d=8$ (impossible), $b=2, d-b =8$, i.e. $d=10$ (impossible), or $b=1, d-b =16$, i.e. $d=17$ (impossible, no triangles);
- $a=4, c=1$. We get $12= b(d-b)$, which means $b=4, d-b =3$, i.e. $d=7$ (impossible), $b=3, d-b =4$, i.e. $d=7$ (impossible), $b=2, d-b =6$, i.e. $d=8$ (impossible), or $b=1, d-b =12$, i.e. $d=13$ (impossible, no triangles);
- $a=4, c=2$. We get $8= b(d-b)$, which means $b=4, d-b =2$, i.e. $d=6$ (impossible), $b=2, d-b =4$, i.e. $d=6$ (impossible), or $b=1, d-b =8$, i.e. $d=9$ (impossible, no triangles);
- $a=4, c=3$. We get $4= b(d-b)$, which means $b=4, d-b =1$, i.e. $d=5$ (impossible), $b=2, d-b =2$, i.e. $d=4$, or $b=1, d-b =4$, i.e. $d=5$ (impossible, 1 triangle in total).
Summing up gives $1+1+2+2+1=7$ cases which we multiply by $2$ to get $14$. In total we found $16+16+16+14 = 62$ triangles.
Answer: 62.
Problem 6
After experimenting with small values for $n$, one can observe that an $n$-gon will either have no reflection symmetries, or have a number of reflection symmetries dividing $n$. The answer can be guessed based on this conjecture: the number of divisors of $2024=2^3\cdot 11 \cdot 23$ is $(3+1)(1+1)(1+1)=16$, so the answer would be $16+1=17$.
The precise proof of the conjecture is rather involved, but we detail it below.
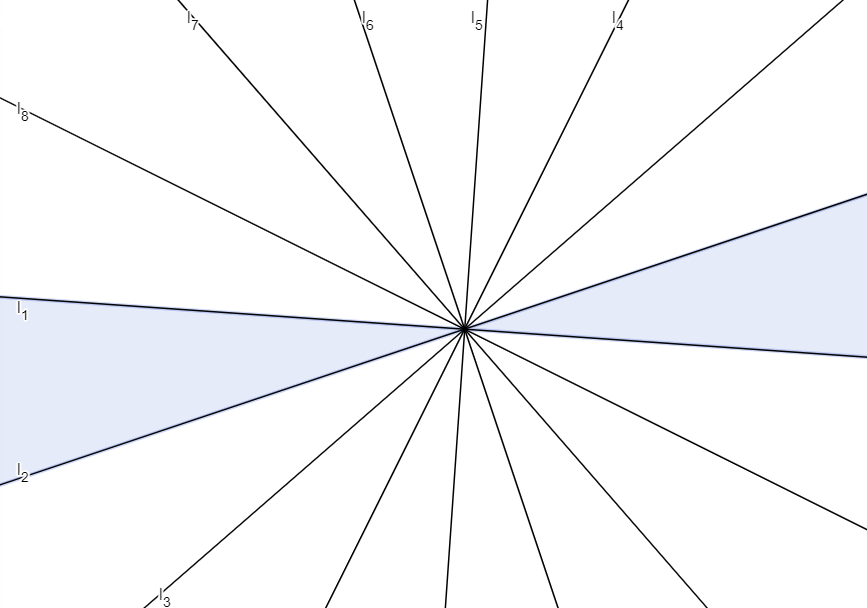
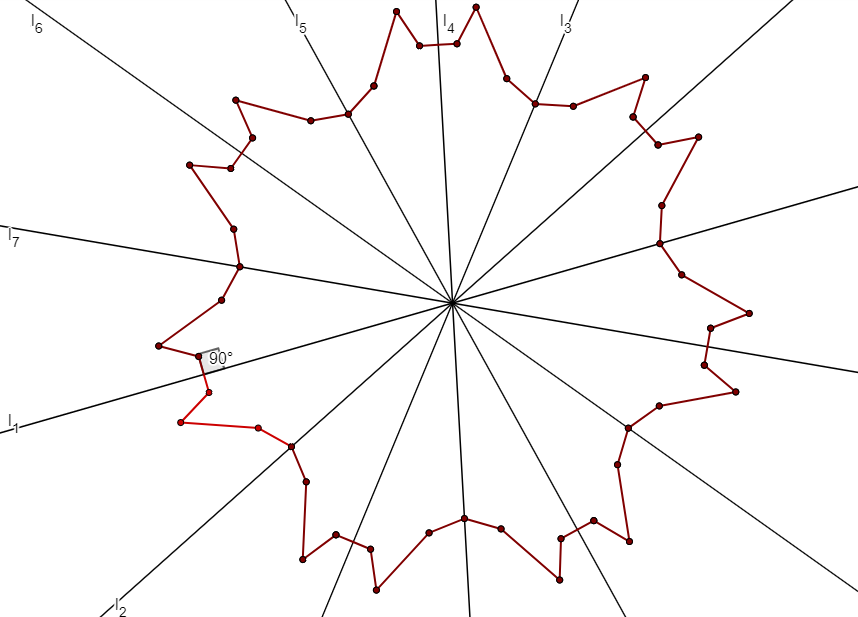
Assume an $n$-gon $P$ has $k>1$ reflection symmetries. Consider the angles of all the different lines of symmetry, and let $\alpha$ be a minimal such angle, say of two lines of symmetry $l_1$ and $l_2$. Denote the image of $P$ under reflection about $l_2$ by $P'$, and the image of $l_1$ under the reflection by $l_1'$. Then $l_1'$ is a line of symmetry for $P'$, but since $P'$ is isometric to $P$, $l_1'$ is also a line of symmetry for $P$. Note that the angle of $l_2$ and $l_1'$ is also $\alpha$, in fact $l_2$ is the bisector of the angle of $l_1$ and $l_1'$. Denote $l_1'$ by $l_3$, reflect $P$ about $l_3$, and denote the image of $l_2$ by $l_4$ under the reflection. Repeating the same argument, we find that $l_4$ is also a line of symmetry for $P$, and $l_3$ is the bisector of the angle of $l_2$ and $l_4$.
Repeating the process, we obtain a sequence of lines $l_1, l_2, \ldots$. We claim that these are all the lines of symmetry of $P$. Assume for contradiction that they are not, and let $e$ be a different line of symmetry. Since any reflection symmetry of $P$ must fix its center of mass, it follows that this point is contained by all lines of symmetry, and hence it is equal to the intersection point $l_1 \cap \ldots \cap l_k \cap \ldots $, which $e$ must also pass through. Assume that $e$ passes through this point between $l_i$ and $l_{i+1}$. Then the angle of $l_i$ and $e$ is less than $\alpha$, contradicting the minimality of $\alpha$.
All that remains is to determine how many different lines appear in the sequence $l_1, l_2, \ldots$. The number of lines of symmetry of any $n$-gon is finite (a symmetry has to take a vertex to a vertex, and there are only $n$ of those), so the sequence eventually repeats. Since any pair of consecutive lines has angle $\alpha$, the angle of $l_i$ and $l_j$ is $\alpha(j-i)$, in particular, we have $l_i=l_j$ if and only if $\alpha(j-i)$ is a multiple of $180$ degrees. It follows that if $l_i=l_j$ with $j >i$, then $l_1=l_{j-i+1}$. So the first repeated element of the sequence is $l_1$, and it is first repeated by $l_{k+1}$ where $k$ is the least integer such that $180$ divides $\alpha k$.
For any $i$, let $p_{i}$ denote the number of vertices of $P$ that fall into the area bounded by the lines $l_{i}$ and $l_{i+1}$ (not including the lines themselves), illustrated below for $i=1$.
Similarly, for any $j$, let $q_{j}$ denote the number of vertices of $P$ that fall on the line $l_{j}$. Notice that $p_1 +p_2 +\ldots +p_{k}+q_1+q_2+ \cdots q_k=n$, the number of all vertices of $P$ by construction. We claim that $p_1=p_2=\ldots =p_k$. Indeed, notice that if we take the segments between $l_i$ and $l_{i+1}$, and reflect it about $l_{i+1}$, then we obtain exactly the segments between $l_{i+1}$ and $l_{i+2}$, and so the number of vertices of $P$ in these areas should be the same, yielding $p_1=p_2=\ldots =p_k$ by induction. For the $q_j$'s, the statement is a little more involved: we have $q_1=q_3=\ldots$ and $q_2=q_4=\ldots$. Indeed, if we reflect the line $l_i$ about $l_{i+1}$, we obtain the line $l_{i+2}$, so it follows that $q_{i}=q_{i+2}$ for all $i$. Since $l_1=l_{k+1}$, we also have $q_1=q_{k+1}$, so in particular if $k$ is odd, then $q_1=q_2=\ldots =q_k$, and if $k$ is even, say $k=2m$, then $q_1=q_3=\ldots=q_{2m-1}$ and $q_2=q_4=\ldots=q_{2m}$. In the $k$ is odd case, it follows that $n=p_1 +p_2 +\ldots +p_{k}+q_1+q_2+ \cdots q_k=k\cdot(p_1+q_1)$, hence $k$ divides $n$. If $k=2m$, then $n=p_1 +p_2 +\ldots +p_{k}+q_1+q_2+ \cdots q_k=kp_1+lq_1+lq_2=m(2p_1+q_1+q_2)$, so it immediately follows that $m$ divides $n$. To show that $k=2m$ divides $n$, we will prove that $q_1$ and $q_2$ are even. Observe that the angle of $l_1$ and $l_{m+1}$ and the angle of $l_{m+1}$ and $l_{2m+1}$ is the same ($m\alpha$ to be precise), so $l_{m+1}$ is a bisector for the angle of $l_1$ and $l_k$, which is a multiple of $180$ degrees. Since $l_{m+1} \neq l_1$, it follows that $l_1=l_k$ and $l_{m+1}$ are perpendicular. So reflecting $l_1$ about $l_{m+1}$ is a symmetry of $P$, and creates a bijection between its vertices on the two halves of $l_1$ on the two sides of the intersection point $l_1 \cap l_{m+1}$. It is easy to see that $l_1 \cap l_{m+1}$ can't be a vertex of $P$ (if it were, it would need to have more than $2$ sides of $P$ adjacent to it), so it follows that $q_1$ is even. The parity of $q_2$ can be deduced similarly. Therefore we have shown that $k$ divides $n$ as needed.
The idea above also gives a method to construct a $n$-gon with exactly $k$ symmetries for any divisor $k$ of $n$, showing one exists for any such $k$. Choose a point $O$ on the plane, and draw $k$ lines $l_1, l_2, \ldots, l_k$ through $O$ in such a way that the angle of $l_i$ and $l_{i+1}$ is $\alpha=180/k$ degrees. It will be convenient to use the notation we had before, and define the infinite sequence $l_1, l_2, \ldots$ where $l_i=l_{i+k}$ for any $i$. These $k$ lines divide the plane into $2k$ connected segments. Choose one of the segments bounded between the line $l_1$ and $l_2$ -- we will construct the part of $P$ that falls into this segment, and construct $P$ by iteratively reflecting this to fill all the segments.
Our strategy will depend on whether $n/k$ is even or odd. If $n/k$ is even, then $n/2k$ is an integer $m$. We will then choose $m$ points $A_1, \ldots, A_m$ in one of the connected segments bounded by $l_1$ and $l_2$, and denote by $P_1$ and $P_2$ the perpendicular projections of $A_1$ to $l_1$ and respectively of $A_m$ to $l_2$. We choose the points $A_1, \ldots, A_m$ in such a way that the polygonal chain $(P_1, A_1, \ldots, A_m, P_2)$ is not self-intersecting, no point $A_i$ has the same distance from $l_1$ and $l_2$, and furthermore the lengths of the segments $A_i O$ are pairwise distinct. This polygonal chain will be the part of the polygon $P$ that falls into the segment.
For each $i$, reflect $A_i$ about $l_2$ to obtain $A_i^2$, then reflect $A_i^2$ about $l_3$ to obtain $A_i^3$, and so on, keep reflecting to construct $A_i=A_i^1, A_i^2, \ldots, A_i^{2k}$. Notice that $A_i^j=A_i^{2k+j}$, furthermore $A_i^{j}$ and $A_i^{k+j}$ fall in between opposite connected segments of $l_{j}$ and $l_{j+1}$ for any $1 \leq j \leq k$. %We can similarly construct $P_i^j$ from $P_i$. Notice furthermore that for even $j$s, $A_1^{j}, P_1^{j+1},$ and $A_1^{j+1}$ are collinear, as are $A_2^{j-1}, P_2^{j},$ and $A_2^{j}$. We then define $P$ to be the polygon $$(A_1, \ldots, A_m, A_m^2, \ldots, A_1^2, \ldots, A_1^{2k-1}, \ldots, A_m^{2k-1}, A_m^{2k}, \ldots, A_1^{2k}).$$ We illustrate the construction below for $m=2$ and $k=8$, which corresponds to $n=32$.
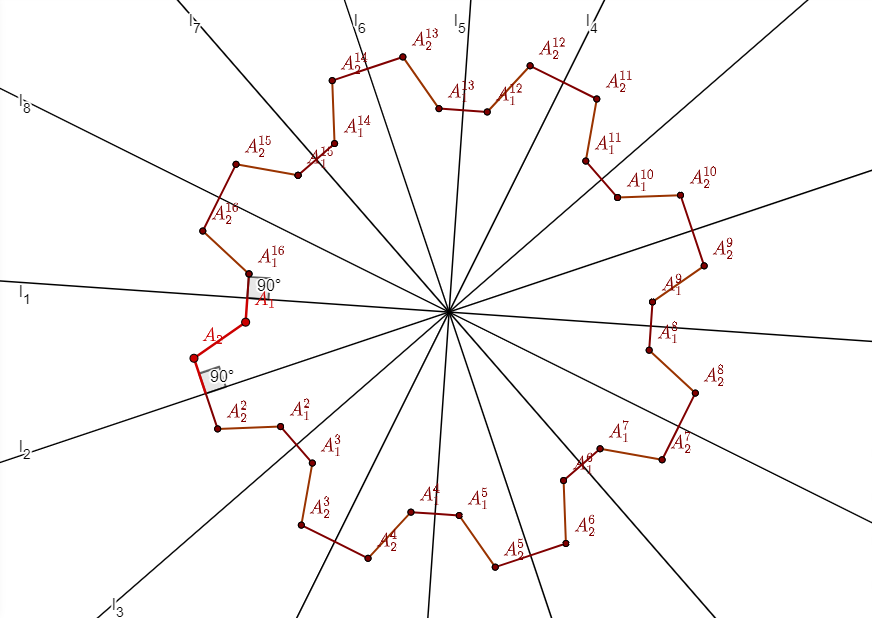
By construction, $P$ has $2k \cdot m=n$ vertices, and all the lines $l_1, \ldots, l_{k}$ are lines of symmetry. We show it has no other lines of symmetry: if it did, say a line $e$, this would necessarily have to pass through the center of mass of $P$, which is the intersection point $O=l_1 \cap \ldots \cap l_k$. Let $A_i^j$ be a vertex of $P$ that does not lie on $e$, moreover choose $A_i^j$ to be of minimal distance from $e$. The image of $A_i^j$ when reflected about $e$ has to be some other vertex $A_x^y$ of $P$. Since $O$ lies on $e$, the segment $OA_x^y$ is the image of the segment $OA_i^j$ under the reflection, in particular, they have the same length, so we must have $i=x$ by our assumption on the choice of points. Notice that if $z$ is an index between $y$ and $j$, then $A_{i}^z$ falls between $A_{i}^j$ and $A_{i}^y$, and so it must be closer to $e$ than $A_i^j$. Since we assumed that the distance of $A_{i}^j$ and $e$ was minimal amongst vertices not on $e$, we must either have that $y$ and $j$ are adjacent indices, or $y=j \pm 2$ and $A_{i}^z$ is on $e$.
In the former case, the line of reflection taking $A_i^j$ to $A_i^y$ is a reflection about one of the lines $l_1, \ldots, l_{k}$, which $e$ then must be equal to. In the latter case, for ease of notation, assume without loss of generality that $z=j+1, y=j+2$. Then $A_i^{j+1}=A_{i}^z$ is the reflection of $A_{i}^j$ about the line $l_j$, hence $d(A_{i}^j,A_{i}^z)=2d(l_j,A_{i}^z)$. Similarly, $A_i^{j+2}=A_{i}^y$ is the reflection of $A_i^{j+1}=A_{i}^z$ about the line $l_{j+1}$, so $d(A_{i}^y,A_{i}^z)=2d(l_{j+1},A_{i}^z)$. But since the reflection about $e$ takes the segment $A_{i}^j A_{i}^z$ into the segment $A_{i}^y A_{i}^z$, these segments must have the same length, and hence the $A_i^{j+1}$ has the same distance form $l_j$ and $l_{j+1}$. But then this would also be true for $A_i$ and $l_1$ and $l_2$, which contradicts our conditions on $A_i$.
We have shown that $P$ is a polygon with exactly $k$ lines of reflection symmetry.
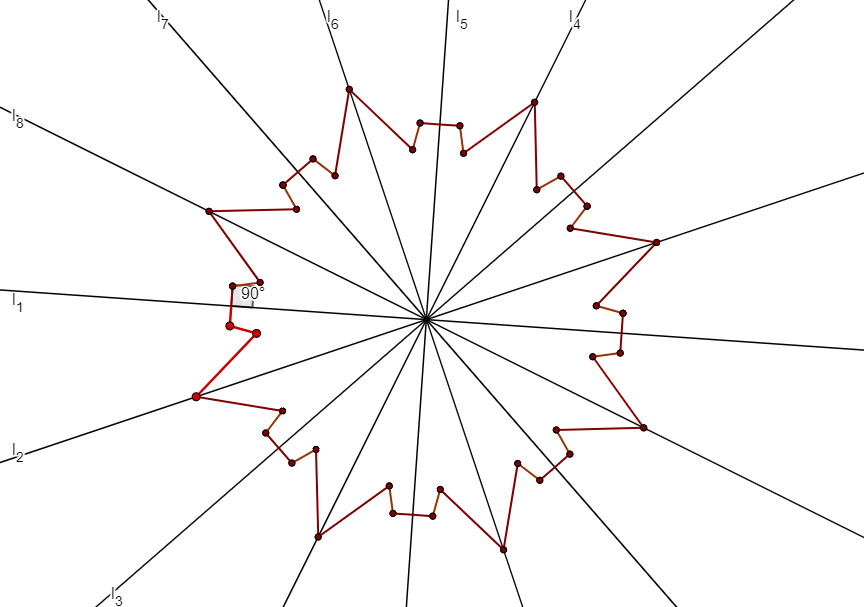
We can use similar constructions for the case when $n/k$ is odd. Write $n=k(2m+1)$ for some even integer $m$. We then will similarly distribute the $2km$ points between the $2k$ segments created by the lines $l_1=l_{k+1}, l_2, \ldots, l_k$, and distribute the remaining $k$ points on the lines themselves.
Again fix a connected segment between $l_1$ and $l_2$, choose $m$ points $A_1, \ldots, A_m$ in the segment, and a point $A_{m+1}$ on the section of $l_2$ bounding the segment. Denote the perpendicular projection of $A_m$ to $l_1$ by $P$, and assume the polygonal chain $(P, A_1, \ldots, A_m, A_{m+1})$ is not self-intersecting, and as before, no point $A_i$ has the same distance from $l_1$ and $l_2$, and furthermore the lengths of the segments $A_i O$ are pairwise distinct. Construct $A_1^j, \ldots, A_{m+1}^j$ as before, and notice that $A_{m+1}^{2i-1}=A_{m+1}^{2i}$ for any $i$. The polygon $P$ is then defined as $$(A_1, \ldots, A_m, A_{m+1}=A_{m+1}^2, A_m^2 \ldots A_1^2, \ldots, A_1^{2k-1}, \ldots, A_m^{2k-1}, A_{m+1}^{2k-1}=A_{m+1}^{2k} A_m^{2k}, \ldots, A_1^{2k}).$$ The number of vertices is then $2km+k=n$ indeed. It has $l_1, \ldots, l_k$ as lines of symmetry by construction, and the fact it has no other reflection symmetries can be proved as in the previous case.
The construction looks slightly different depending on whether $k$ is even or odd: when $k$ is odd, each line $l_i$ contains a single vertex of $P$, and when $k$ is even, each line $l_{2i}$ contains two vertices of $P$, whereas the lines of odd indices contain none.
We illustrate the construction below for $m=2$ and $k=8$, which gives $n=40$, and for $m=3$ and $k=7$, which gives $n=49$.
This shows that a $2024$-gon with $k$ reflection symmetries, where $k \geq 1$, exists if and only if $k$ divides $2024$. Lastly, observe that there are $n$-gons with no symmetries: choose an $n$-gon $A_1=A_{n+1}, A_2, \ldots, A_n$ in such a way that the lengths of the segments $A_i A_{i+1}$ are pairwise different. Symmetries take sides to sides of equal length, so such a polygon cannot have any.
Answer: 17.
Problem 7
Let us denote by $C(m,n)$ the number of possible arrangements of $m$ skipping ropes with $n$ crossings. We will determine $C(6,9)$ recursively.
For $m$ ropes held by $2m$ children, label the children in the both lines from $1$ through $m$, so that the children with equal numbers are lined up opposite each other. We can then describe the $m$ skipping ropes as pairs $(k,l)$, where the rope $(k,l)$ is held by child $k$ in the first line and child $l$ in the second line.
With this setup, we may see that two distinct ropes $(k,l)$ and $(p,q)$ cross each other if and only if either:
- $k < p$ and $q < l$, or;
- $p < k$ and $l < q$.
Write our list of $m$ ropes as $(1,e_1), (2,e_2), \ldots (m, e_m)$. Notice that $e_1,e_2,\ldots, e_m$ is a permutation of the numbers $1,2,\dots,m$, and each permutation determines a different arrangement of the skipping ropes, so the arrangements correspond exactly to permutations of $1,2,\dots,m$. There are $m!$ such permutations.
In the list $e_1,e_2,\ldots, e_m$, a crossing pair of ropes corresponds to a pair of these integers which are ``out-of-order", that is ropes $(i,e_i)$ and $(j,e_j)$ cross if $i < j$ but $e_j < e_i$. In particular, the rope $(1, e_1)$ will cross exactly those ropes $(j, e_j)$ where $e_j < e_1$, that is, when $e_j=1, 2 \ldots, e_1-1$. There are $e_1-1$ such ropes.
Now suppose an arrangement of $m$ ropes has crossing number $n$, and let us think about what happens if we remove the first rope from the arrangement. We will now have $m-1$ ropes remaining, and the crossing number is $n-(e_1-1)=n-e_1+1$. There are, by definition, $C(m-1, n-e_1+1)$ such rope arrangements. The number $C(m,n)$ then can be expressed as a sum of the values $C(m-1, n-e_1+1)$ for all possible choices of $e_1$. Note that $1 \leq e_1 \leq m$, but we also have $n \geq e_1-1$ (the number of all crossings cannot be lower than the number of crossing introduced by the first rope), so $1 \leq e_1 \leq \min(m, n+1)$. Thus we obtain a recursion $$C(m,n)=\sum_{e_1=1}^{\min(m, n+1)} C(m-1, n-e_1+1)=C(m-1,n) + \ldots + C(m-1, \max(0,n-m+1)).$$
We can use the following table to compute $C(6,9)$, filled from the top: it is clear that $C(2,0) = 1, C(2,1) = 1$ and all other $C(2,n)$ values are zero, and each line can be obtained from the line above using the recursive formula.
| $m \downarrow n$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 2 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 3 | 5 | 6 | 5 | 3 | 1 | 0 | 0 | 0 |
| 5 | 1 | 4 | 9 | 15 | 20 | 22 | 20 | 15 | 9 | 4 |
Thus, we get $C(6,9) = 4+ 9+ 15+20+22+20 = 90$. Meanwhile, the total number of arrangements is $6! = 720 $. Thus, the probability we are looking for is $\frac{90}{720} = 0.125$.
Answer: 0.125
Problem 8
We first need to find what composition of notes the ambassador took with him, that is, find the minimal number of 1s and doublers needed to compose every value between $1$ and $3000$, while minimizing the number of 1 dollar notes used. In order to do this, we first need to understand how a stack of a given value can be composed using as few notes, and as few 1 dollar notes as possible. We will refer to stacks with this property as optimal stacks.
A simple observation is that an optimal stack will always have $1$ on its top, as doublers on top add nothing to the value of the stack and can be removed to create a smaller stack with the same value.
We next observe that an optimal stack never has two consecutive 1 dollar notes. Indeed, suppose we have a stack with two consecutive 1s, we will show that we can compose a stack with the same value using less 1 dollar notes and no more notes overall, and hence such stack can't be optimal. The following observation will be useful: if we have a stack where the topmost $k$ notes form a stack of value $V$, then replacing the top $k$ notes with an arbitrary stack with the same value $V$ will not change the overall value of the big stack.
If there are two consecutive 1s are on the top, then the value of the top two notes is $(1+1)=2$. A $1$ dollar note followed by a doubler has the same value $(1 \cdot 2)= 2$, so we could replace the top two $1$ dollar notes by a $1$ and a doubler to obtain a stack with the same value, using less $1$s, and no more notes overall.
If there are two consecutive 1 dollar notes lower down in the stack, let us consider the topmost such pair, say at positions $n$ and $n+1$. Then the $(n-1)$th note will necessarily be a doubler (otherwise they would not be the topmost pair), so the value of the top $n+1$ notes will be $((V \cdot 2) +1+1)=(2V+2)$, where $V$ is the value of the stack composed of the first $n-2$ notes. By replacing the sequence $doubler, 1, 1$ by $1, doubler$, the top $n+1$ notes the same value $(V+1)\cdot 2=(2V+2)$. So again we obtain a stack with the same value, but using less $1$s and less notes overall.
Now let us consider an optimal stack. Suppose the stack has $k$ 1 dollar notes, and denote the number of doublers between the $j$th and $j+1$th $1$ dollar notes by $n_j$ for $1 \leq j \leq k-1$ (these are all positive), and let $n_k$ denote the number of doublers following the $k$th $1$ dollar note (this can be $0$). The value of the stack will then be $$((((1 \cdot \underbrace{2\cdot 2 \cdots 2}_{n_1})+1)\cdot \underbrace{2\cdot 2 \cdots 2}_{n_2} )+1)\cdots \underbrace{2\cdot 2 \cdots 2}_{n_k})=$$ $$=2^{n_1+\cdots +n_k}+2^{n_2+\cdots +n_k}+\cdots +2^{n_k},$$ where $n_1 +\cdots +n_k > n_2+\cdots +n_k > \ldots > n_k \geq 0$. Denoting the exponent $n_i +\cdots +n_k$ by $a_i$ for $1 \leq i \leq k$, the value of the stack is the sum $$2^{a_1}+2^{a_2}+\cdots +2^{a_k}$$ of $k$ distinct powers of $2$. There is only one way to decompose a positive integer into a sum of distinct powers of $2$: this is given by the binary form of the number (hinted at by the name Binarnia). The binary form of $2^{a_1}+2^{a_2}+\cdots +2^{a_k}$ has $a_1+1$ digits and $k$ ones, at the positions $a_1, a_2, \ldots, a_k$ (where the rightmost digit has position $0$). It follows that the optimal stack for any given value $V$ is unique, and can be derived from its binary form. The number of digits in the binary form determines the value $a_1=n_1+\cdots +n_k$, which is exactly the number of all doublers in the optimal stack. The number of $1$ dollar notes in the optimal stack is equal to $k$, that is, the number of $1$ digits in the binary form of the number $V$.
The binary form of $3000$ is $101110111000_2$. It has $12$ digits, therefore any integer $1 \leq n \leq 3000$ will have binary form with at most $12$ digits as well. The most "costly" number below $3000$ is the $11$-digit binary number consisting of ones, $11111111111_2=2^{11}-1=2047$. This requires $11-1=10$ doublers and $11$ ones.
We claim that these notes suffice to compose a stack of any value up to $3000$. It is clear that any integer value between $1$ an $2047$ can be composed, as the binary form of any such number has at most $11$ digits needing at most $10$ doublers, and at most $11$ ones. We can also compose $12$-digit numbers which have at most $10$ ones using a "sub-optimal" stack. The optimal stack for such a number will always begin with the sequence $1, double$, but we can replace this by a $1, 1$-sequence without changing the stack's value, as observed above. This uses only $10$ doublers and at most $11$ ones, which we have. Since the least binary number with $12$ digits and $11$ ones is $101111111111_2>101110111000_2=3000$, we can indeed obtain any value up to $3000$.
After the bus rides, the ambassador has $10$ doublers and $9$ one dollar notes. So he can no longer compose those values for which he needed $10$ or $11$ ones. These are those binary numbers betwwen $1$ and $3000$ which contain
- $11$ ones;
- $10$ ones;
- $12$ digits and $9$ ones.
Let us consider the binary numbers with $11$ ones. If such a number has $12$ digits, then it either begins with $11$ or is equal to $101111111111_2$, both are bigger than $101110111000_2=3000$. So the only binary number between $1$ and $3000$ with $11$ one digits is $11111111111_2=2047$ -- that is one amount the ambassador can no longer pay for.
Let us now consider the binary numbers between $1$ and $3000$ with $10$ ones. If such a number has $12$ digits, then to be smaller than $101110111000_2$, it can only begin with
- $100$, in which case it must $100111111111_2$, or
- $1010$, in which case it must be $101011111111_2$, or
- $10110$, in which case it must be $101101111111_2$.
If the binary number has $11$ digits or less, then it has $10$ ones and at most $1$ zero. There are $11$ such numbers ($10$ of these have $11$ digits, and one is $1111111111_2$) and all are between $1$ and $3000$.
Lastly let us consider those $12$-digit binary numbers between $1$ and $3000$ which contain $9$ ones. As before, these need to begin with either
- $100$, in which case we have $9$ choices for the position of the remaining $0$, or
- $1010$, in which case we have $8$ choices for the position of the remaining $0$, or
- $10110$, in which case we have $7$ choices for the position of the remaining $0$, or
- $1011100$, in which case it must be $101110011111_2$, or
- $10111010$, in which case it must be $101110101111_2$, or
- $101110110$, in which case it must be $101110110111_2$.
Altogether, there are $1+(3+11)+(9+8+7+1+1+1)=42$ amounts the ambassador can no longer pay for, so he can still pay the remaining $3000-42=2958$ values.
Answer: 2958
© The University of Manchester 2012–2024, All Rights Reserved
Contact us | Privacy notice
