Solutions
Problem 1
Let the decimal form of $n$ be $\overline{a_{2022} \ldots a_1a_0}$, where $a_{2022} \neq 0$. There are $9 \cdot 10^{2022}$ such numbers. If in the process of adding $25$ to $n$, no carries are made, then $s(n+25)=s(n)+s(25)=s(n)+7$. However, if during the summation a $1$ is carried over from the $k$th digit to the $k+1$th, then during the operation a number $x$ was added to the $k$th digit $a_k$ with $a_k+x \geq 10$, changing the digits $a_{k+1},\ a_k$ to $a_{k+1}+1,\ a_k+x-10$, which decreases the sum of digits by $9$ compared to what it would have been without a carry. This shows that $s(n+25)=s(n)+7-9c$ where $c$ is the number of carries made during the summation. If $s(n+25)-s(n)=-11$, then we must have $c=2$. We proceed by a case separation according to the positions from where the two carries were made. Case 1: from $k=0$ and $k=1$. In this case $a_0+5 \geq 10$ (for the first carry) and $a_1+2+1 \geq 10$ (for the second carry; notice that both the $2$ of the $25$ and the $1$ carried over from $a_0$ are added to $a_1$). As no more carries happen, $a_2+1 \leq 9$. This means $a_0$ can take the $5$ different values between $5-9$, $a_1$ can take the $3$ different values between $7-9$, and $a_2$ can take the $9$ different values between $0-8$, which gives $5 \cdot 3 \cdot 9 \cdot 10^{2019} \cdot 9$ numbers. Case 2: from $k=1$ and $k=2$. In this case $a_0+5 \leq 9$ (no carry), $a_1+2 \geq 10$ (for the first carry), $a_2+1 \geq 10$ (for the second carry), and since no more carries happen, $a_3+1 \leq 9$. So $a_0$ can take the $5$ different values between $0-4$, $a_1$ can take the $2$ values between $8-9$, $a_2$ can only be $9$, and $a_3$ can take $9$ different values between $0-8$. This gives $5 \cdot 2 \cdot 1 \cdot 9 \cdot 10^{2018} \cdot 9$ numbers. There are no more possibilities – if no digits are carried from a position $k$ where $k \neq 0$, then $a_{k+1}$ is unchanged and hence no digits are carried further either. So the above cases are all the possible cases where $2$ carries happen. Hence the ratio we are looking for is $$p=\frac{5 \cdot 3 \cdot 9 \cdot 10^{2019} \cdot 9+5 \cdot 2 \cdot 1 \cdot 9 \cdot 10^{2018} \cdot 9}{9 \cdot 10^{2022}}=\frac{135+9}{1000}=0.144.$$
Problem 2
Let $S_1$ and $S_2$ be the two given sequences of $99$ different symbols on the door. Frodo's task is to `transform' $S_1$ into $S_2$ by changing one symbol at a time, always arriving to a sequence of pairwise different symbols. First notice that if there are two symbols, say $a$ and $b$, which occupy the same two positions in both $S_1$ and $S_2$ but in reversed order, then it takes at least three steps to facilitate that switch: $$\ldots a \ldots b \ldots \to \ldots a \ldots c \ldots \to \ldots b \ldots c \ldots \to \ldots b \ldots a \ldots,$$ where $c$ is a symbol not occurring in the first sequence. This shows that if $S_1=a_1 a_2 \ldots a_{98} b$ and $S_2=a_2 a_1 a_4 a_3 \ldots a_{98} a_{97} b'$, at least $3\cdot 98/2=147$ steps are needed to switch the first $98/2$ pairs, and one step to change $b$ to $b'$, thus at least $148$ steps are needed to get from $S_1$ to $S_2$. We show that $148$ is indeed sufficient for any pair of sequences by describing a procedure which always uses at most that many steps. First, we check if $S_1$ and $S_2$ contain the exact same $99$ symbols. If this is not the case, i.e. $S_2$ contains a symbol $b$ in the $i$th position that does not occur in $S_1$, then we replace the $i$th symbol of $S_1$ by $b$, so the obtained sequence now agrees with $S_2$ in position $i$. By iterating this step, we eventually arrive at a sequence $S_1'$ that contains exactly the same symbols as $S_2$. Notice that if made $k$ changes at this stage, then $S_1'$ and $S_2$ now agree in at least $k$ positions. We now move on to the second part of the procedure we call rearranging. Choose any symbol of $S_1'$ that is not at the same position in $S_2$. Suppose this symbol $b_1$ is in position $i_1$ in $S_1'$ and $i_2$ in $S_2$. First replace $b_1$ with a new symbol $c$ in $S_1'$. Then $b_1$ no longer occurs in the obtained sequence so we can put it into its desired position, $s_2$. Denote the symbol we have overwritten by $b_2$ – as this symbol now no longer occurs in the sequence, we can put this symbol into its desired position as well, overwriting another symbol $b_3$. We keep iterating this until the symbol we override does not occur in $S_2$ – this can only be if the symbol we overwrite is the newly added symbol $c$. In this case, we stop. In every step, except for the very first one in which we introduced $c$, we put a new symbol into its desired position. So if we took $l$ steps, the new sequence $S_1''$ and $S_2$ agree in $l-1$ more positions than before. Note that we must have $l \geq 3$. The `swapping' algorithm in the first paragraph is an example of rearranging when $l=3$. A longer example, where $l=4$, would be $$S_1'=\ldots b_1 \ldots b_2 \ldots b_3\ldots,\ S_2=\ldots b_3 \ldots b_1 \ldots b_2\ldots,$$ $$\begin{array}{l} \ldots b_1 \ldots b_2 \ldots b_3 \ldots \to \ldots c \ldots b_2 \ldots b_3 \ldots \to \ldots c \ldots b_1 \ldots b_3 \ldots \to \\ \ldots c \ldots b_1 \ldots b_2 \ldots \to \ldots b_3 \ldots b_1 \ldots b_2\ldots \end{array}. $$ Notice that $S_1''$ and $S_2$ still contain the exact same symbols and agree in more positions than before. We repeat the `rearranging' procedure until they eventually agree everywhere. If the different iterations of rearranging took $l_1, l_2, \ldots, l_m$ steps, then altogether $$k+l_1+\cdots +l_m$$ steps were taken, altogether resulting in $$k+(l_1-1)+\cdots +(l_m-1)=k+l_1+\cdots l_m-m$$ positions of agreement, so $k+l_1+\cdots +l_m-m \leq 99$, that is we took $99-m$ steps at most. If we want to maximize the number of steps taken, we have to maximize $m$ – this can be done by choosing $l_1=\ldots =l_m=3$ and $k$ as small as possible, which makes $m=49$ and $k=1$. The number of steps for these numbers is exactly $148$ indeed. The number of new lines Frodo has to carve is then $148-1=147$.
Problem 3
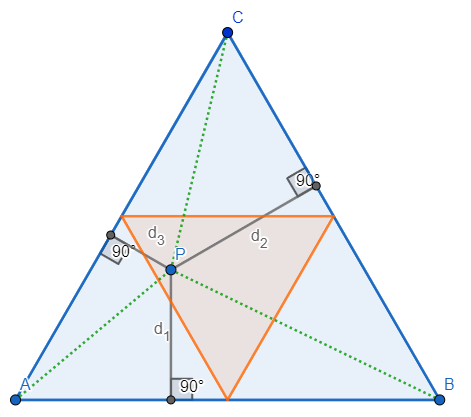
The segments of length $d_1, d_2$ and $d_3$ form a triangle if and only if the sum of any two is at least as large as the third. Denote the vertices of the equilateral triangle by $A,B$ and $C$ so that the distances $d_1,d_2, d_3$ are exactly the heights of the triangles $ABP$, $BCP$ and $CAP$ respectively. Thus, denoting the common side length of $ABC$ by $a$, these triangles have areas
$$T_{ABP}=d_1\cdot\frac{a}{2},\ T_{BCP}=d_2\cdot\frac{a}{2},\ T_{CAP}=d_3\cdot \frac{a}{2},$$
and thus for example $d_1+d_2 \geq d_3$ holds if and only if $T_{ABP}+T_{BCP} \geq T_{CAP}$. Since $T_{ABP}+T_{BCP}+T_{CAP}=T_{ABC}$, the inequality can be rewritten as
$T_{ABC}-T_{CAP} \geq T_{CAP}$, that is, $T_{ABC} \geq 2T_{CAP}$. As $T_{ABC}=\frac{ah}{2}$ where $h$ is the height of $ABC$, we immediately obtain $\frac{ah}{2} \geq ad_3$, that is, $\frac{h}{2} \geq d_3$, which means $P$ should lie between the side $CA$ and the segment connecting the midpoints of $AB$ and $BC$.
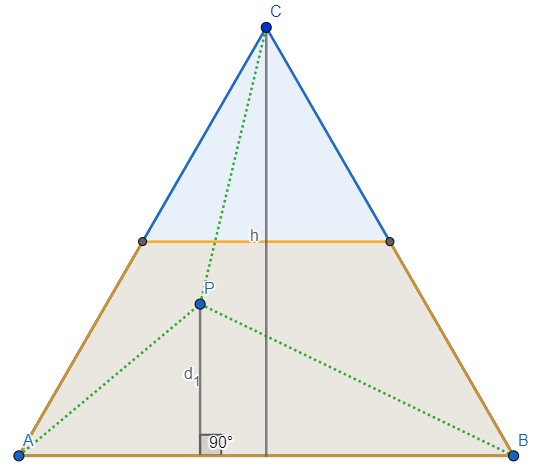 Similarly, the conditions of $d_1+d_3 \geq d_2$ and $d_2+d_3 \geq d_1$ become $\frac{h}{2} \geq d_2$ and $\frac{h}{2} \geq d_1$ respectively, therefore $d_1, d_2$ and $d_3$ form a triangle if and only if $P$ is contained in the triangle determined by the midpoints of the sides $AB, BC$ and $AC$. The area of this triangle is exactly fourth of the area of $ABC$, the probability of $P$ falling inside this triangle is therefore $0.25$.
Similarly, the conditions of $d_1+d_3 \geq d_2$ and $d_2+d_3 \geq d_1$ become $\frac{h}{2} \geq d_2$ and $\frac{h}{2} \geq d_1$ respectively, therefore $d_1, d_2$ and $d_3$ form a triangle if and only if $P$ is contained in the triangle determined by the midpoints of the sides $AB, BC$ and $AC$. The area of this triangle is exactly fourth of the area of $ABC$, the probability of $P$ falling inside this triangle is therefore $0.25$.
Problem 4
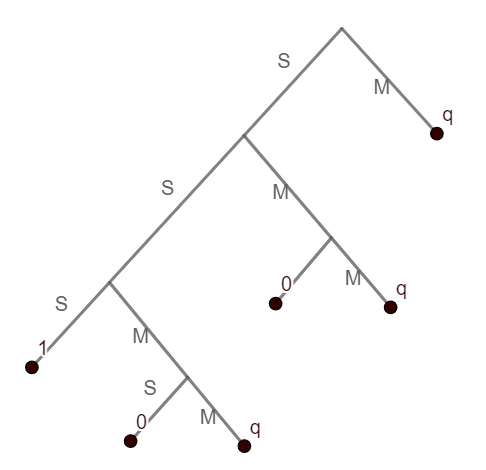
Let us introduce notation: in the sequence of Casey's shots, successful ones will be denoted by $S$, missed ones by $M$. If the bet is fair, then Alex and Blair both win with the same probability $1/2$. In order to determine the correct value of $p$, let us determine the probability that Alex wins as a function of $p$. Given a $p$, let $q$ denote the probability that Alex wins. Notice if the first shot is a miss, then no sequence of the form SSS or SMS can involve the first shot, so in this case, after the first shot, the probability of Alex winning is still the same $q$. However, if the first shot is S, various things can happen:
- if it is followed by SS, Alex wins
- if it is followed by MS, Alex loses
- if it is followed by MM, then second M cannot be part of any sequence SSS or SMS, so just as in the previous case, the probability of Alex winning after the third shot is again $q$
- if it is followed by SMS, then Alex loses
- if it is followed by SMM, then again we are back where we started and Alex wins with probability $q$.
Problem 5
If we did not have the constraint about the 100 given points, the answer would be easy: to get the biggest possible number of intersections, we draw 2023 pairwise intersecting lines (i.e. each pair of lines intersect) in such a way that no three lines intersect at the same point. This would give $\frac{2023\cdot 2022}{2}$ intersections (each of the 2023 lines intersects all 2022 other lines, but this counts intersections twice). However, these conditions cannot be achieved if all lines have to pass through one of the $100$ given points, as $100 < \frac{2023}{2}$ forces that some of these points will have at least $3$ lines passing through them. If $k \geq 3$ lines all intersect at the same point, then instead of the $\frac{k(k-1)}{2}$ pairwise different intersections between themselves that they contributed to the number $\frac{2023\cdot 2022}{2}$, they would only contribute $1$ intersection, so $\frac{k(k-1)}{2}-1$ intersection points are lost. It is clear that we lose the least number of intersections if every line goes through exactly one of the 100 points, and there are no three lines intersecting at any other point. This can certainly be achieved by adding lines one by one in such a way that existing intersection points, and lines determined by the any two of the 100 points are avoided.
If we have $k_1, k_2, \ldots, k_{100}$ pairwise intersecting lines each passing through exactly one of the $100$ points in such a way that no three lines intersect at any other point, then we can calculate the number of intersection points in by subtracting the `lost' intersections from $\frac{2023\cdot 2022}{2}$, which gives
$$\frac{2023\cdot 2022}{2}-\left(\frac{k_1(k_1-1)}{2}-1\right)-\left(\frac{k_2(k_2-1)}{2}-1\right)- \cdots -\left(\frac{k_{100}(k_{100}-1)}{2}-1\right).$$
In order the maximize this formula, we have to minimize the sum
$$S=\frac{k_1(k_1-1)}{2}+\frac{k_2(k_2-1)}{2}+\ldots +\frac{k_{100}(k_{100}-1)}{2}.$$
Rearranging, we have
$$2S=k_1^2+\cdots +k_{100}^2-(k_1+\cdots+ k_{100})= k_1^2+\cdots +k_{100}^2-2023,$$
so minimizing $S$ boils down to minimizing $k_1^2+\cdots +k_{100}^2$ when $k_1+\cdots+ k_{100}=100$. It can be seen experimentally and intuitively that this sum is minimal when the $k_i$s are as close to being equal as possible, e.g. if $k_1=\ldots =k_{77}=20$ and $k_{78}=\ldots=k_{100}=21$ (as $77 \cdot 20 +23 \cdot 21=2023)$; below we also give a formal proof, which is in essence the well-known proof of the inequality between the arithmetic and quadratic means.
Notice that
$$ k_1^2+\cdots +k_{100}^2=(k_1+\ldots +k_{100})^2-\sum_{1 \leq i < j\leq 100}2k_{i}k_j, $$
hence
$$\begin{eqnarray}
100(k_1^2+\cdots +k_{100}^2) & = & 2023^2+99(k_1^2+\cdots +k_{100}^2)-\sum_{1 \leq i < j\leq 100}2k_{i}k_j \\
&=&2023^2+\sum_{1 \leq i < j\leq 100}(k_i-k_j)^2,
\end{eqnarray}$$
making $k_1^2+\cdots +k_{100}^2$ minimal when $\sum_{1 \leq i < j\leq 100}(k_i-k_j)^2$ is minimal, i.e. when the differences between the $k_i$s are the smallest. This is indeed achieved by choosing $k_1=\ldots =k_{77}=20$ and $k_{78}=\ldots=k_{100}=21$.
The formula then gives
$$\frac{2023\cdot 2022}{2}-77\cdot \left(\frac{20\cdot 19}{2}-1\right)-23\left(\frac{21\cdot 20}{2}-1\right)=2025893.$$
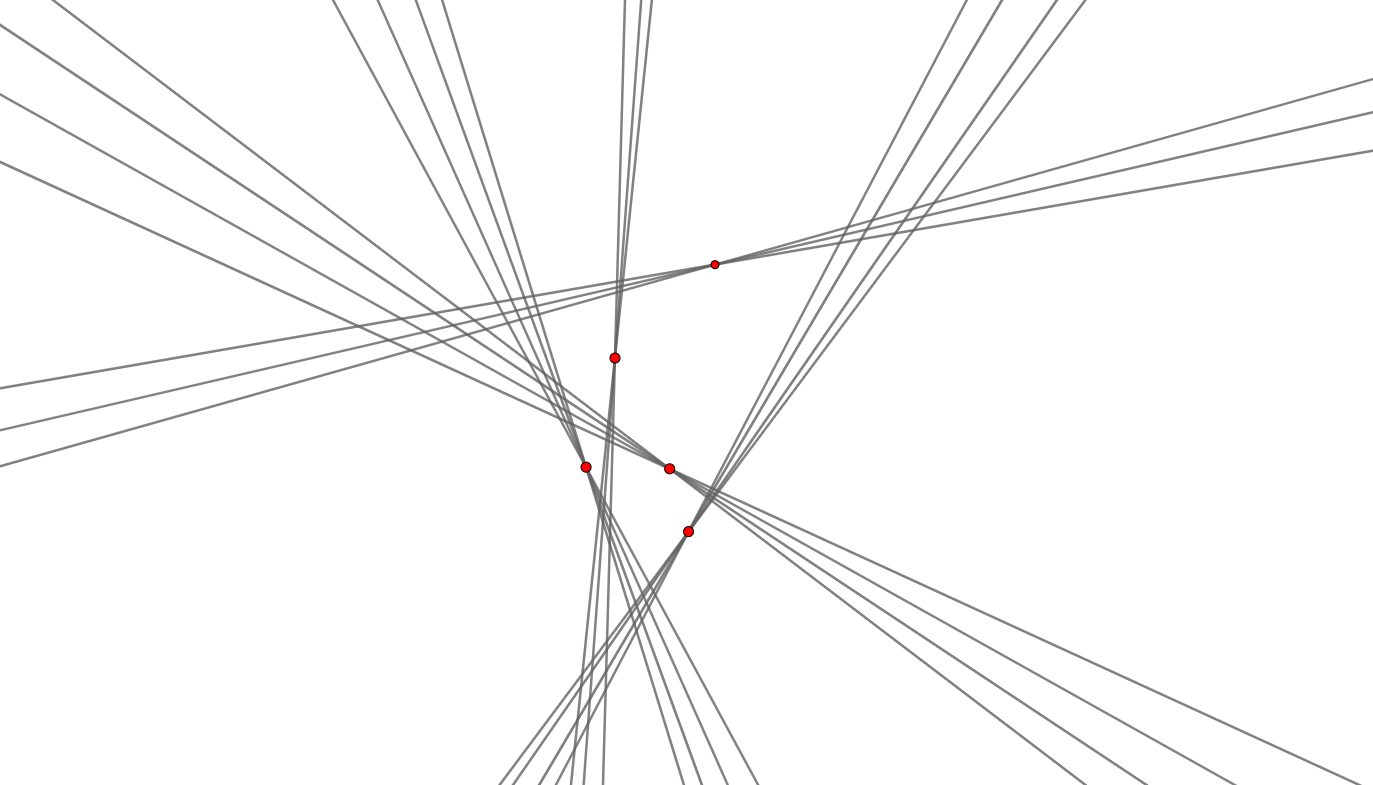
The above construction for 5 points and 18 lines.
Problem 6
For any given roll of the die, the gain (that is, the payout minus the $2$ dollars) is a number $a,b,c,d,e$ or $f$, depending on which number was rolled. Notice that the gain need not be positive. Let us examine the gain after $3$ rolls. This is determined by the combination of numbers rolled. Since the probability of a given combination depends on whether that combination consists of $3$ different numbers, $2$ different numbers or just $1$ number, we separate the number of possible roll sequences along these cases. If the die is rolled 3 times, then either
- all $3$ rolls are different – there are $6 \choose 3$ choices for the combination of numbers, which can be ordered in $3!$ ways, giving $6\cdot 5\cdot 3=90$ such possibilities,
- $2$ rolls are the same whilst one is different – there are $6 \cdot 5$ choices for the combination of numbers, which can be ordered in $3$ ways, giving $6\cdot 5\cdot 3=90$ such possibilities,
- all $3$ rolls are the same – there are $6$ such possibilities.
- $a$ or $b$; $c,d$ or $e$; $f$, which yields $2 \cdot 3 \cdot 1 \cdot 3!=36$ cases,
- $a$ or $b$; $f$; $f$, which yields $2\cdot 3=6$ cases,
- $a$ or $b$, $e$; $e$, which yields $2\cdot 3=6$ cases,
- $b$; $d$; $e$, which yields $3!=6$ cases,
Problem 7
First notice that as the ball bounces off a wall, its centerpoint behaves like a pointlike object bouncing off an imaginary line parallel to the walls. Therefore without loss of generality we may continue to think about the football as pointlike object.
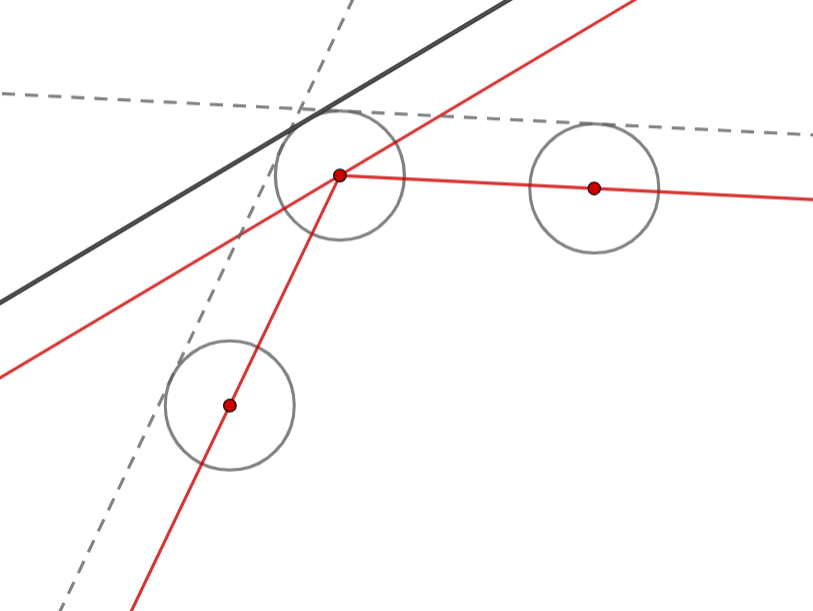 Since the football rolled back at Carlos from the exact same direction he kicked it in, it must be that the ball reversed its full trajectory after zigzagging towards the corner. So, by denoting the position of the $i$th bounce by $P_i$, we have that $P_1=P_{29}$, $P_{2}=P_{28}$ and so on, $P_{i}=P_{30-i}$ in general. In particular, since $P_{14}=P_{16}$, the incoming angle of the ball when reaching $P_{15}$ must have been perpendicular to the wall.
We can recursively determine the rest of the incoming angles starting from $P_{15}$. Suppose the angle of the two walls is $\alpha$, and denote the corner of the angle by $O$. Let the incoming angle at $P_{n}$ ($n \leq 14$) be $\beta_{n}$ (see image). Notice that the $P_{14}OP_{15}$ triangle is right angled, so $\beta_{14}=90^\circ-\alpha$, and denoting by $\gamma_{14}$ the degree of the incoming and outgoing trajectory, we have
$\gamma_{14}+2\beta_{14}=180^\circ$, which makes
$$\gamma_{14}=180^\circ-2\beta_{14}=180^\circ-2(90^\circ-\alpha)=2\alpha.$$
Looking at the $P_{15}P_{14}P_{13}$ right angled triangle, we have
$$\beta_{13}=90^\circ-\gamma_{14}=90^\circ-2\alpha,$$
and it follows that
$$\gamma_{13}=180^\circ-2(90^\circ-2\alpha)=4\alpha.$$
Since the football rolled back at Carlos from the exact same direction he kicked it in, it must be that the ball reversed its full trajectory after zigzagging towards the corner. So, by denoting the position of the $i$th bounce by $P_i$, we have that $P_1=P_{29}$, $P_{2}=P_{28}$ and so on, $P_{i}=P_{30-i}$ in general. In particular, since $P_{14}=P_{16}$, the incoming angle of the ball when reaching $P_{15}$ must have been perpendicular to the wall.
We can recursively determine the rest of the incoming angles starting from $P_{15}$. Suppose the angle of the two walls is $\alpha$, and denote the corner of the angle by $O$. Let the incoming angle at $P_{n}$ ($n \leq 14$) be $\beta_{n}$ (see image). Notice that the $P_{14}OP_{15}$ triangle is right angled, so $\beta_{14}=90^\circ-\alpha$, and denoting by $\gamma_{14}$ the degree of the incoming and outgoing trajectory, we have
$\gamma_{14}+2\beta_{14}=180^\circ$, which makes
$$\gamma_{14}=180^\circ-2\beta_{14}=180^\circ-2(90^\circ-\alpha)=2\alpha.$$
Looking at the $P_{15}P_{14}P_{13}$ right angled triangle, we have
$$\beta_{13}=90^\circ-\gamma_{14}=90^\circ-2\alpha,$$
and it follows that
$$\gamma_{13}=180^\circ-2(90^\circ-2\alpha)=4\alpha.$$
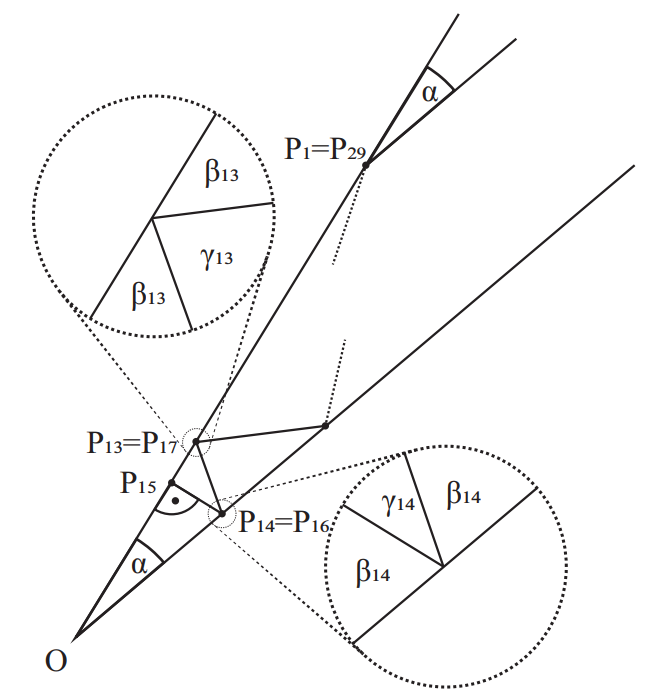 From here, we can prove by an inductive argument that
$\beta_n=90^\circ-(15-n)\alpha$ and $\gamma_n=2(15-n)\alpha$ for any $n=14,13\ldots, 1$ – we have seen that it holds for $n=14,13$. Notice that the angles of the $P_{n}P_{n-1}P_{n-2}$ triangle are $\beta_{n}, \gamma_{n-1}, \beta_{n-2}$, so $\beta_{n-2}=180^\circ-\beta_n-\gamma_{n-1}$. Applying the inductive hypothesis for $\beta_n$ and $\gamma_{n-1}$, we have
$$\beta_{n-2}=180^\circ-(90^\circ-(15-n)\alpha)-2(15-n+1)\alpha=90^\circ-(15-n+2)\alpha$$
indeed, and
$$\gamma_{n-2}=180^\circ-2\beta_{n-2}=180^\circ-2(90^\circ-(15-n+2)\alpha)=2(15-n+2)\alpha.$$
So the incoming angle at $P_1$ is $90^\circ-14\alpha$, and since the incoming trajectory is parallel to one of the walls, we must have $90^\circ-14\alpha=\alpha$, which gives $\alpha=6^\circ\approx 0.10472$ rad.
From here, we can prove by an inductive argument that
$\beta_n=90^\circ-(15-n)\alpha$ and $\gamma_n=2(15-n)\alpha$ for any $n=14,13\ldots, 1$ – we have seen that it holds for $n=14,13$. Notice that the angles of the $P_{n}P_{n-1}P_{n-2}$ triangle are $\beta_{n}, \gamma_{n-1}, \beta_{n-2}$, so $\beta_{n-2}=180^\circ-\beta_n-\gamma_{n-1}$. Applying the inductive hypothesis for $\beta_n$ and $\gamma_{n-1}$, we have
$$\beta_{n-2}=180^\circ-(90^\circ-(15-n)\alpha)-2(15-n+1)\alpha=90^\circ-(15-n+2)\alpha$$
indeed, and
$$\gamma_{n-2}=180^\circ-2\beta_{n-2}=180^\circ-2(90^\circ-(15-n+2)\alpha)=2(15-n+2)\alpha.$$
So the incoming angle at $P_1$ is $90^\circ-14\alpha$, and since the incoming trajectory is parallel to one of the walls, we must have $90^\circ-14\alpha=\alpha$, which gives $\alpha=6^\circ\approx 0.10472$ rad.
Problem 8
First, observe that tent number $1$ can only be last if tent number $2$ was the first to have been occupied. Indeed, assume that $k$ was the tent occupied first. The first tent with number less than $k$ to be occupied would then be tent number $1$, as that is the furthest from both $k$ and any number larger than $k$. But if $k \geq 3$, then that would mean tent number $2$ is occupied after tent $1$. If tent number $2$ is occupied first – this has probability $1/2023$ – then the next tent occupied is $2023$, and tent $1$ will continue to remain empty as long as there are tents available with empty neighbours. Once there are no such tents remaining, denote by $p$ the number of empty tents left. These $p$ tents are then filled up completely randomly, so the probability that tent $1$ ends up last is $1/p$. Thus all we need to do to solve the problem is show that the value of $p$ does not depend on the order the parcels are rented in. We will determine the value of $p$ recursively. If we have a row of $n+1$ tents numbered $t, t+1, \ldots, t+n$ for some integer $t$, with the tents $t$ and $t+n$ occupied initially but all other tents empty, then as they start filling up (according to the same rules as before), let $g(t,t+n)$ denote the number of empty tents left when the last tent with empty neighbours is occupied. Thus $p=g(2,2023)+1$ – the number of empty tents in the $(2,2023)$ interval, plus tent number $1$. It is at this point not clear that $g(t,t+n)$ is well-defined, i.e. independent of the order in which the empty tents are occupied, but it is clear that if well-defined, it is independent of $t$, so let us put $f(n)=g(t,t+n)$. The goal is then to determine $p=f(2021)+1$. We can determine $f(n)$ for small values by hand (and for these, we can also check the function is indeed well-defined): $f(2)=1, f(3)=2, f(4)=2$. For larger $n$s, we determine $f(n)=g(0,n)$ recursively. If $n=2k$, then the first tent occupied in the interval $(0,2k)$ is tent number $k$. Thus $f(2k)=g(0,2k)=g(0,k)+g(k,2k)=2f(k)$. If $n=2k+1$, then the first tent occupied is either the $k$th or the $k+1$th with $0,5-0,5$ probability. In the former case, $f(2k+1)=g(0,k)+g(k,2k+1)=f(k)+f(k+1)$, in the latter case $f(2k+1)=g(0,k+1)+g(k+2,2k+1)=f(k+1)+f(k)$, thus we get the same formula in both cases. This also shows, by induction, that the value of $f$ does not depend on the choices made. The recursive formula allows us to calculate $f(2023)$ directly: $$\begin{eqnarray} f(2023)&=&f(1011)+f(1012)=f(505)+3f(506)=f(252)+7f(253)=9f(126)+7f(127)=\\ &=&25f(63)+7f(64)=25f(31)+39f(32)=25f(15)+103f(16)=25f(7)+231f(8)=\\ &=&25f(3)+487f(4)=25\cdot 2+487 \cdot 2=1024 \end{eqnarray}$$ We remark that there is also a closed formula for $f(n)$, namely $f(n)=2^{\lfloor\log_2n \rfloor}$, which the interested reader may try to prove. To finish the solution, the probability is then $$\frac{1}{2023}\cdot \frac{1}{p}=\frac{1}{2023}\cdot \frac{1}{f(2022)+1}=\frac1{2023\cdot 1025}=\frac1{2073575}\approx 0.0000004823.$$
© The University of Manchester 2012–2023, All Rights Reserved
Contact us | Privacy notice
