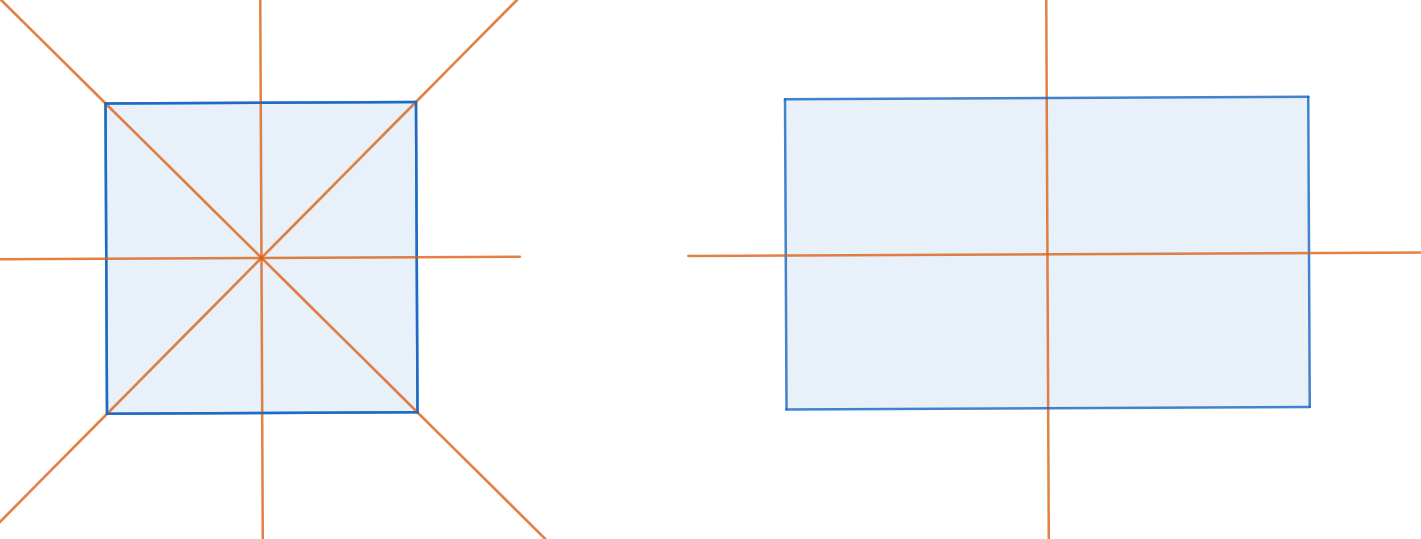
Given a polygon $P$, let $f(P)$ denote the number of lines of reflection symmetries of $P$. For example, if $P$ is a square, then $f(P)=4$, and if $P$ is rectangle that is not a square, then $f(P)=2$. For how many different values $n$ does there exist a $2024$-gon $P$ with $f(P)=n$?

Mathsbombe Competition 2024 is organised by the The Department of Mathematics at The University of Manchester.
© The University of Manchester 2012–2024, All Rights Reserved
Contact us | Privacy notice