Problem 3

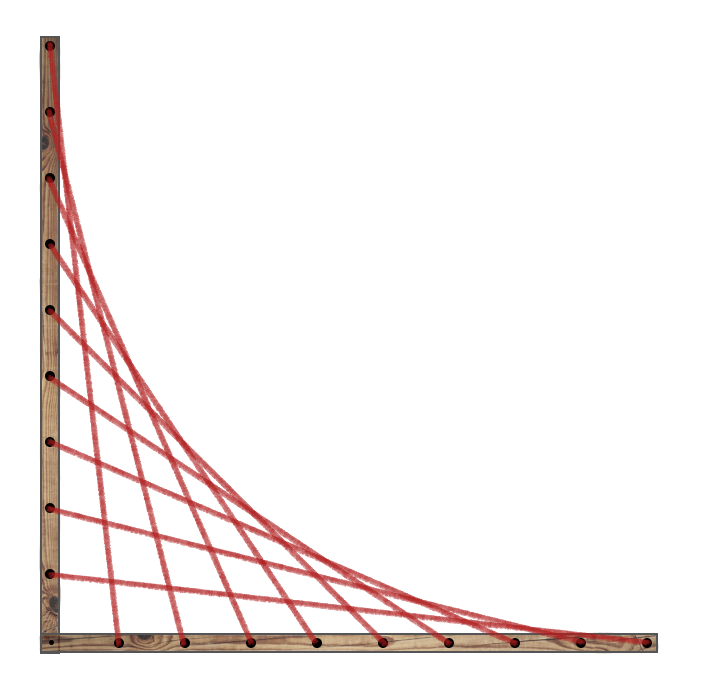
Alex is creating string art in the following way: he takes two long pieces of wood joined together in a right angle at one end, and drills an equal number of holes along both, in straight lines. On both pieces, the last drilled hole is 20 centimeters away from the point of joining, and the holes are spaced evenly between themselves and the point of joining. Alex then ties a string from the outermost hole of the vertical piece to the innermost hole of the horizontal piece, then another string from the second outermost hole of the vertical piece to the second innermost hole of the horizontal piece, and so on. When he is finished, the edge of the string pattern will trace a curve. The more holes Alex drills, the smoother this curve will be. If he were physically able to drill holes and attach strings to every point along the two lines, the strings would trace a perfectly smooth curve. Plotting this imaginary curve in a coordinate system where the axes correspond to the lines traced by the holes in the wooden pieces, and each centimeter corresponds to a unit, what is the $y$-coordinate of the curve for $x=\pi$? Give your answer rounded to 4 decimal places.

The picture illustrates the string are described in the question: two long pieces of wood joined together in a right angle, with an equal number of holes drilled along both, and strings tied between the holes in the pattern described in the question.