• HomePage
• WikiSandbox

Vortices

Stability

• Ring
• Ring + pole
• Aligned rings
• Staggered rings
• Ring + 2 poles

Hyperbolic plane

PmWiki

• Initial Setup Tasks
• Basic Editing
• Documentation Index
• PmWiki FAQ
• PmWikiPhilosophy
• Release Notes
• ChangeLog

pmwiki.org

• Cookbook (addons)
• Skins (themes)
• PITS (issue tracking)
• Mailing Lists

Login

Ring and two poles \(C_{nv}(R,\,2p)\)

In the graphs, the horizontal axis is \(\kappa_N\), the vertical is \(\kappa_S\).

\(\theta_0\) is the colatitude of the ring (so \(\theta_0=\pi/2\) lies on the equator); all are for the ring lying in the Northern hemisphere.

Lyapounov stable points in red elliptic ones in blue

The grey line in the figures for \(n\geq4\) is the instability boundary given by the higher modes.

n=2

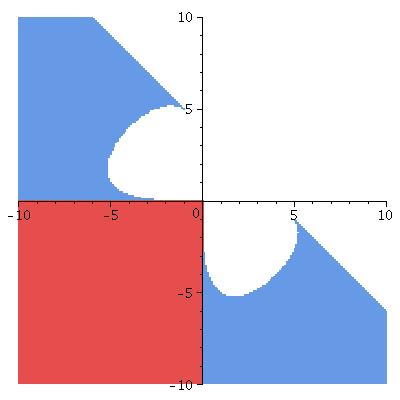
θ₀ = π/2 (= 1.57)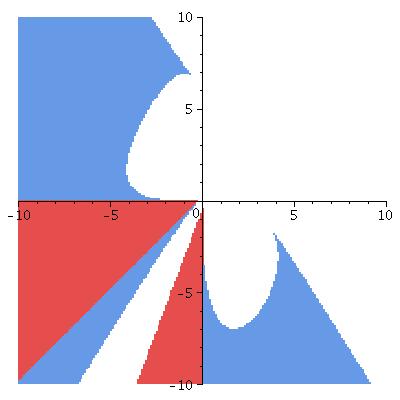

θ₀ = 1.45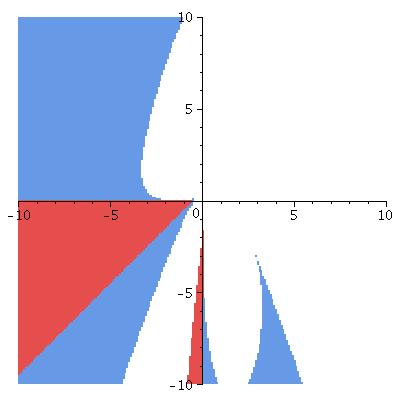

θ₀ = 1.3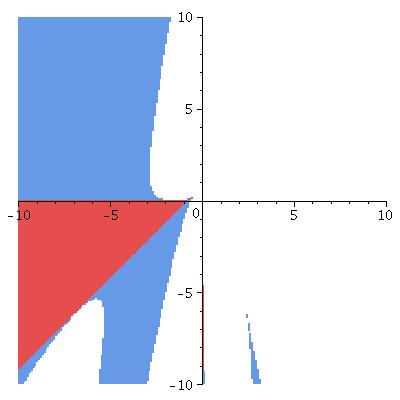

θ₀ = 1.15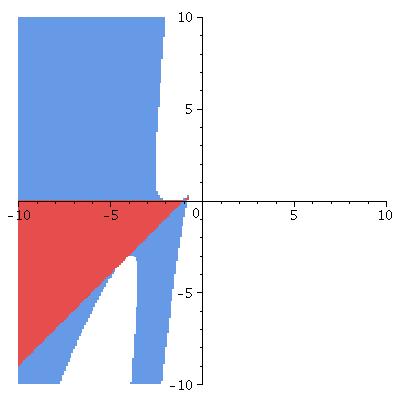

θ₀ = 1.0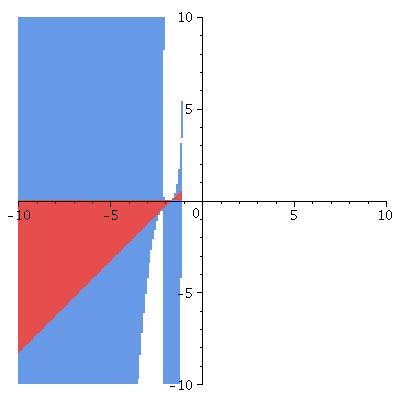

θ₀ = 0.5

n=3

With \(|\kappa_j| \leq 10\) (zoomed in)

θ₀ = π/2 (= 1.57)

θ₀ = 1.45

θ₀ = 1.3

θ₀ = 1.0

θ₀ = 0.5

n = 3 with \(|\kappa_j| \leq 50\) (zoomed out)

θ₀ = π/2 ( = 1.57)

θ₀ = 1.5

θ₀ = 1.3

θ₀ = 1.0

θ₀ = 0.5

n=4

Zoomed in: \(|\kappa_j|\leq 10\)

θ₀=π/2 (= 1.57)

θ₀=1.45

θ₀=1.3

θ₀=1.0

θ₀=0.75

θ₀=0.5

Zoomed out: \(|\kappa_j|\leq 50\)

θ₀=π/2 (= 1.57)

θ₀=1.45

θ₀=1.3

θ₀=1.0

θ₀=0.75

θ₀=0.5

n=5

\(|\kappa_j|\leq 10\)

θ₀ = π/2 (= 1.57)

θ₀ = 1.45

θ₀ = 1.3

θ₀ = 1.0

\(|\kappa_j|\leq 50\)

θ₀ = π/2 (= 1.57)

θ₀ = 1.45

θ₀ = 1.3

θ₀ = 1.0

n=12

\(|\kappa_j|\leq 50\)

θ₀ = π/2 (= 1.57)

θ₀ = 1.4

\(|\kappa_j|\leq 100\)

θ₀ = π/2 (= 1.57)

θ₀ = 1.4